16. Пусть элементы x 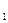 ,x
,x 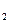 ,…,x
,…,x 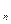 ,…,y
,…,y 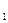 ,y
,y 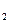 ,…,y
,…,y 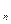 ,… удовлетворяют условию x
,… удовлетворяют условию x 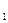 <x
<x 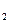 <…<x
<…<x 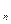 <…<y
<…<y 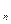 <…y
<…y 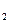 <y
<y 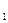 и пусть для любого положительного элемента e>0, начиная с некоторого номера n, выполняются условия y
и пусть для любого положительного элемента e>0, начиная с некоторого номера n, выполняются условия y 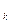 -x
-x 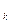 < e, k = n, n+1, …. Тогда существует элемент Z такой, что при всех значениях n выполняется x
< e, k = n, n+1, …. Тогда существует элемент Z такой, что при всех значениях n выполняется x 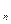 < Z < y
< Z < y 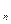 .
.
То, что элемент Z, о котором говорится в этой аксиоме, является единственным, несложно доказать от противного.
Определение 2.
Множество R называется множеством действительных чисел, а его элементы действительными числами, если они удовлетворяют всем тем же аксиомам 1-15, что и рациональные числа и, дополнительно, аксиом непрерывности Кантора.
 2015-05-18
2015-05-18 1251
1251








