Построить представление чисел, в котором иррациональные числа приближаются рациональными числами наилучшим образом. Рациональная дробь p/q приближает иррациональное число a наилучшим образом, если для любого рационального числа m/n с n£q выполняется равенство |a-p/q| < |a-m/n|.
Рассмотрим десятичные приближения. Пусть m = a 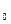 , a
, a 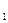 , …,a
, …,a 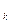 - десятичное приближение с “k” знаками после запятой числа a = a
- десятичное приближение с “k” знаками после запятой числа a = a 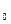 , a
, a 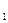 , …,a
, …,a 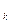 ,a
,a 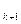 ,…. Тогда погрешность этого измерения определяется разностью:
,…. Тогда погрешность этого измерения определяется разностью:
|a-m/n| = a 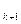 /10
/10 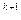 +a
+a 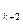 /10
/10 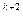 +…<9/10
+…<9/10 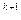 (1+1/10+…) = 9/10
(1+1/10+…) = 9/10 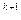 ´
´
1/(1-1/10) = 1/10 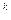 ~1/n.
~1/n.
Для более лучших приближений используется представление иррационального числа цепной дробью, [6]. Если p/q - конечная цепная дробь, приближающая число a, то [6], стр. 46, |a-p/q| < 1/q 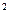 .
.
Таким образом, представление числа цепной дробью «более экономично», чем представление десятичной дробью.
Напомним, что до сих пор не найдены эффективные алгоритмы арифметических операций для представлений чисел в виде цепных дробей, [6], стр. 29-30.
 2015-05-18
2015-05-18 301
301








