Пример 1. Пусть система аксиом Т состоит из 14 аксиом аксиоматики Гильберта, определяющих абсолютную геометрию плоскости (геометрию без аксиомы параллельности)

Пусть система аксиом Т состоит из 14 аксиом аксиоматики Гильберта, определяющих абсолютную геометрию плоскости (геометрию без аксиомы параллельности). Мы имеем две реализации этой планиметрии:

(1) арифметическая модель R² (евклидовой плоскости);

(2) модель Пуанкаре L₂ (плоскости Лобачевского). Можно установить взаимно однозначное соответствие между точками М 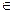R² и точками N 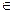L₂, а также между прямыми l 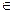R² и прямыми a 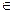L₂. В то же время не всем отношениям между точками и прямыми в L₂ можно найти соответствующие отношения в R². Например, отношение Ð(a₁, a₂)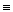 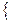прямые a₁ и a₂ не параллельны и не пересекаются 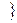может выполняться в L₂ и не имеет аналога в R². (Другие неевклидовы отношения между точками и прямыми на плоскости L₂ см. в п. 5.2 §5).