Парная регрессия и корреляция
В регрессионном анализе рассматривается односторонняя стохастическая зависимость случайной переменной у от одной (или нескольких) неслучайной независимой переменной х.
Рассмотрим линейную модель и представим ее в виде
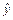 = b 0 + b 1 x. (1)
= b 0 + b 1 x. (1)
Для решения поставленной задачи определим формулы расчета неизвестных параметров уравнения линейной регрессии (b 0, b 1) используя метод наименьших квадратов (МНК).
Согласно МНК неизвестные параметры b 0 и b 1 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi от значений 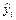 , найденных по уравнению регрессии (1), была минимальной:
, найденных по уравнению регрессии (1), была минимальной:
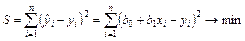 . (2)
. (2)
На основании необходимого условия экстремума функции двух переменных S = S (b 0, b 1) (4) приравняем к нулю ее частные производные, откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии. Затем, разделив обе части уравнений системы на n, получим систему нормальных уравнений в следующем виде:
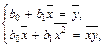 (3)
(3)
где соответствующие средние определяются по формулам:
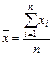 ; (4)
; (4) 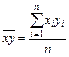 ; (6)
; (6)
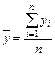 ; (5)
; (5) 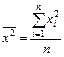 . (7)
. (7)
Решая систему (3), найдем
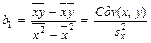 , (8)
, (8)
где 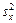 - выборочная дисперсия переменной х:
- выборочная дисперсия переменной х:
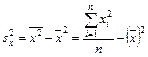 , (9)
, (9)
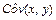 - выборочный корреляционный момент или выборочная ковариация:
- выборочный корреляционный момент или выборочная ковариация:
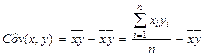 . (10)
. (10)
Коэффициент b 1 называется выборочным коэффициентом регрессии Y по X.
Коэффициент регрессии у по х показывает, на сколько единиц в среднем изменяется переменная у при увеличении переменной х на одну единицу.
Для двух случайных переменных можно определить выборочный коэффициент корреляции, который является показателем тесноты связи.
Если r > 0 (b 1 > 0), то корреляционная связь между переменными называется прямой, если r < 0 (b 1 < 0), - обратной.
Формулы для расчета коэффициента корреляции имеют следующий вид:
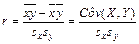 ; (11)
; (11)
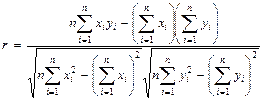 . (12)
. (12)
Выборочный коэффициент корреляции обладает следующими свойствами:
1.Коэффициент корреляции принимает значения на отрезке [-1: 1], т.е. -1 ≤ r ≥ 1.
2.При r =±1 корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдения располагаются на прямой линии.
3. При r = 0 линейная корреляционная связь отсутствует. При этом линия регрессии параллельна оси ОХ.
В силу воздействия неучтенных факторов и причин отдельные наблюдения переменной у будут в большей или меньшей мере отклоняться от функции регрессии j(х). В этом случае уравнение взаимосвязи двух переменных (парная регрессионная модель) может быть представлена в виде:
у = j(х) + e,
где e - случайная переменная (случайный член), характеризующая отклонение от функции регрессии.
Отметим основные предпосылки регрессионного анализа (условия Гаусса-Маркова).
1. В модели yi = b0 + b1 xi + e i возмущение e i есть величина случайная, а объясняющая переменная xi – величина неслучайная.
2. Математическое ожидание возмущения e i равно нулю:
M (e i) = 0. (13)
3. Дисперсия возмущения e i постоянна для любого i:
D (e i) = s2. (14)
4. Возмущения e i и e j не коррелированны:
M (e i e j) = 0 (i ¹ j). (15)
5. Возмущения e i есть нормально распределенная случайная величина.
Оценкой модели yi = b0 + b1 xi + e i по выборке является уравнение регрессии 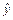 = b 0 + b 1 x. Параметры этого уравнения b 0 и b 1 определяются на основе МНК. Воздействие неучтенных случайных факторов и ошибок наблюдений в модели определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии.
= b 0 + b 1 x. Параметры этого уравнения b 0 и b 1 определяются на основе МНК. Воздействие неучтенных случайных факторов и ошибок наблюдений в модели определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии.
Теорема Гаусса-Маркова. Если регрессионная модель
yi = b0 + b1 xi + e i удовлетворяет предпосылкам 1-5, то оценки b 0, b 1 имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
Таким образом, оценки b 0 и b 1 в определенном смысле являются наиболее эффективными линейными оценками параметров b0 и b1.
Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Для проверки значимости выдвигают нулевую гипотезу о надежности параметров.
Нулевая гипотеза Н 0 – это основное проверяемое предположение, которое обычно формулируется как отсутствие различий, отсутствие влияние фактора, отсутствие эффекта, равенство нулю значений выборочных характеристик и т.п.
Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой.
Коэффициент регрессии (b 1) является случайной величиной. Отсюда после вычисления возникает необходимость проверки гипотезы о значимости полученного значения. Выдвигаем нулевую гипотеза (Н 0) о равенстве нулю коэффициента регрессии (Н 0: b 1 = 0) против альтернативной гипотезы (Н 1) о неравенстве нулю коэффициента регрессии (Н 1: b 1 ¹ 0). Для проверки гипотезы Н 0 против альтернативы используется t -статистика, которая имеет распределение Стьюдента с (n - 2) степенями свободы (парная линейная регрессия).
Коэффициент регрессии надежно отличается от нуля (отвергается нулевая гипотеза Н0), если t набл > t a; n -2. В этом случае вероятность нулевой гипотезы будет меньше выбранного уровня значимости. t a; n -2 - критическая точка, определяемая по математико-статистическим таблицам.
Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.
Согласно основной идее дисперсионного анализа
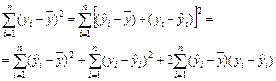 (16)
(16)
или
Q = QR + Qe, (17)
где Q – общая сумма квадратов отклонений зависимой переменной от средней, а QR и Qe – соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов.
Схема дисперсионного анализа имеет вид, представленный в табл. 1.
Средние квадраты 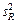 и s 2 (табл. 1) представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной х и воздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров уравнения регрессии; п – число наблюдений.
и s 2 (табл. 1) представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной х и воздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров уравнения регрессии; п – число наблюдений.
При отсутствии линейной зависимости между зависимой и объясняющими(ей) переменными случайные величины 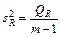 и
и 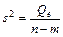 имеют c2-распределение соответственно с т – 1 и п – т степенями свободы.
имеют c2-распределение соответственно с т – 1 и п – т степенями свободы.
Таблица 1
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средние квадраты |
| Объясненная | 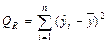 | m – 1 | 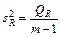 |
| Остаточная | 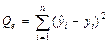 | n – m | 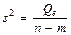 |
| Общая | 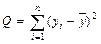 | n – 1 |
Поэтому уравнение регрессии значимо на уровне a, если фактически наблюдаемое значение статистики
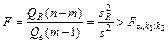 , (18)
, (18)
где 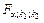 - табличное значение F -критерия Фишера-Снедекора, определяемое на уровне значимости a при k 1 = m – 1 и k 2 = n – m степенях свободы.
- табличное значение F -критерия Фишера-Снедекора, определяемое на уровне значимости a при k 1 = m – 1 и k 2 = n – m степенях свободы.
Учитывая смысл величин 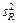 и s 2, можно сказать, что значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.
и s 2, можно сказать, что значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.
Для парной линейно регрессии т = 2, и уравнение регрессии значимо на уровне a (отвергается нулевая гипотеза), если
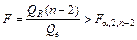 . (19)
. (19)
Следует отметить, что значимость уравнения парной линейной регрессии может быть проведена и другим способом, если оценить значимость коэффициента регрессии b 1, который имеет t -распределение Стьюдента с k = n – 2 степенями свободы.
Уравнение парной регрессии или коэффициент регрессии b 1 значимы на уровне a (иначе – гипотеза Н 0 о равенстве параметра b 1 нулю, т.е.
Н 0: b 1 = 0, отвергается), если фактически наблюдаемое значение статистики
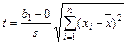 (20)
(20)
больше критического (по абсолютной величине), т.е. | t | > t 1 - a; n - 2.
Коэффициент корреляции r значим на уровне a (Н 0: r = 0), если
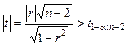 . (21)
. (21)
Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле:
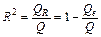 . (22)
. (22)
Величина R 2 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.
В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату корреляции, т.е. R 2 = r 2.
 2015-05-18
2015-05-18 3364
3364