(1) 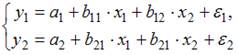
(2) 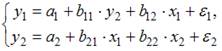
(3) 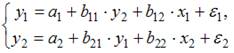
| система независимых уравнений | |
| система рекурсивных уравнений | |
| система одновременных уравнений | |
| система нормальных уравнений |
ТЕОРИЯ: Условия идентифицируемости уравнения системы:
Необходимое условие (но недостаточное):
D – число экзогенных (предопределенных, Х) переменных, которые содержатся в системе, но не входят в данное уравнение;
H – число эндогенных (Y) переменных в данном уравнении.
D+1=H – уравнение идентифицируемо
D+1<H – уравнение неидентифицируемо
D+1>H – уравнение сверхидентифицируемо
Достаточное условие:
1) Определитель матрицы из коэффициентов переменных (эндогенных и экзогенных), отсутствующих в данном уравнении, не равен нулю;
2) Ранг этой матрицы не меньше, чем число эндогенных (Y) в системе без 1.
Укажите необходимое и достаточное условие, характеризующее первое уравнение системы одновременных уравнений. Укажите не менее двух вариантов ответа
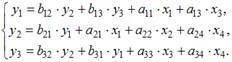
| 1 Необходимое условие – по счетному правилу первое уравнение точно идентифицируемо |
| 2 Достаточное условие выполнено – первое уравнение идентифицируемо |
| 3 Необходимое условие – по счетному правилу первое уравнение сверх идентифицируемо |
| 4 Необходимое условие – по счетному правилу первое уравнение неидентифицируемо |
| 5 Достаточное условие не выполнено: первое уравнение неидентифицируемо |
 2015-05-18
2015-05-18 427
427







