Принцип “ближайшего соседа”

Решение задачи:

В Excel 7.0 создаем таблицу с исходными данными и таблицы (матрицы) с расчетами (табл.10).

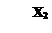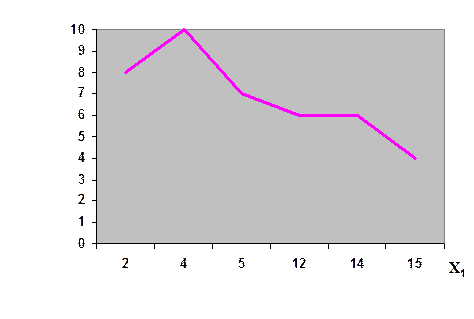Рис. 12. Зависимость между объемом выпускаемой продукции и среднегодовой стоимостью основных промышленно-производственных фондов

Воспользуемся агломеративным иерархическим алгоритмом классификации. В качестве расстояния между объектами примем обычное евклидовое расстояние. Тогда согласно формуле:

,

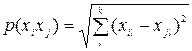где l - признаки; k - количество признаков, расстояние между объектами 1 и 2 равно:

р₁₁=0; .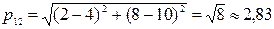

Расчеты последующих расстояний 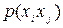аналогичны.

1. Формулу: =КОРЕНЬ((B5-B5)^2+(B6-B6)^2) помещаем в ячейку В14 и рассчитываем расстояние р₁₁, затем в ячейке В15 - расстояние р₁₂ по формуле: =КОРЕНЬ((B5-C5)^2+(B6-C6)^2) и т.д., пока не будет произведен расчет расстояний между всеми шестью объектами (ячейки В14:В29):

p₁₁=0; p₁₂=2.83; p₁₃=3.16; p₁₄=10.20; p₁₅=12.17;

p₁₆=13.6; p₂₃=3.16; p₂₄=8.94; p₂₅=10.77; p₂₆=12.53;

p₃₄=7.07; p₃₅=9.06; p₃₆=10.44; p₄₅=2; p₄₆=3.61; p₅₆=2.24.

2. Полученные данные помещаем в таблицу (матрицу) -ячейки D15:J21. Из матрицы расстояний следует, что объекты 4 и 5 наиболее близки P₄₅=2.00 и поэтому объединяются в один кластер. Для расчета наименьшего расстояния используется формула: =МИН(F16:J16;G17:J17;H18:J18;I19:J19;J20) - ячейка E22.

После объединения имеем пять кластеров.

3. Матрицу расстояний помещаем в ячейки D25 - I30, воспользуемся этой матрицей расстояний, чтобы рассчитать расстояние объединяемых объектов 4,5 и 6, которые имеют наименьшее расстояние P_MIN=P_4,5,6=2.24 (формула =МИН(F26:I26;G27:I27;H28:I28;I29 в ячейке E32). После объединения имеем четыре кластера: S₍₁₎, S₍₂₎, S₍₃₎, S_(4,5,6).

Таблица 10

Исходные данные

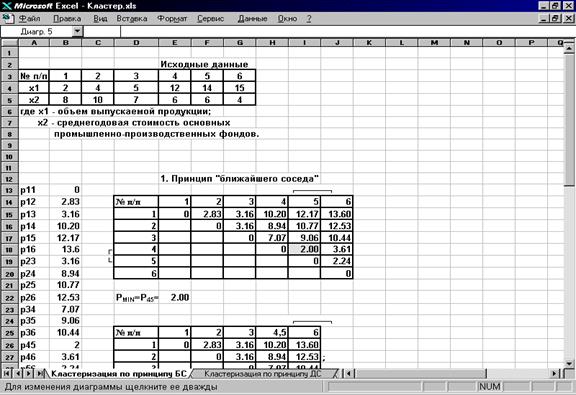
4. Вновь находим матрицу расстояний (табл.11), помещаем рассчитанные значения в ячейки D35 - H39 и объединяем объекты 1 и 2, имеющие наименьшее расстояние P_MIN=P_1,2=2.83 (формула =МИН(F36:H36;G37:H37;H38) в ячейке E41). Расстояние между остальными кластерами остается без изменения. В результате имеем три кластера: S_(1,2), S₍₃₎, S_(4,5,6).

5. Объединим теперь объекты 1,2 и 3, расстояние между которыми равно: P_MIN=P_1,2,3=3.16 (формула =МИН(F45:G45;G46) в ячейке E49.

6. Таким образом, при проведении кластерного анализа по принципу “ближайшего соседа” получили два кластера: S_(1,2,3), S_(4,5,6), расстояние между которыми равно:

P_{(1,2,3); (4,5,6)} = 7,07.

Таблица 11

Расчетные значения

Результаты иерархической классификации объектов представлены на рис.13 в виде

дерева объединения кластеров - дендрограммы, где по оси ординат приводятся расстояния между объединяемыми на данном этапе кластерами.

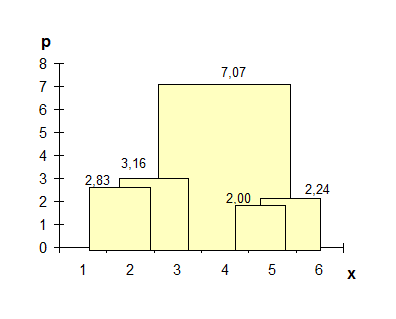
Рис.13. Дендрограмма