2015-05-18
304
В прикладных задачах часто используются различные преобразования Фурье функций непрерывного аргумента, а также представлений функций с помощью сходящихся тригонометрических рядов. Всякую непрерывно дифференцируемую функцию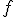 
можно разложить в ряд Фурье:
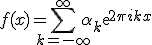
коэффициенты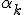 
находятся по следующим формулам
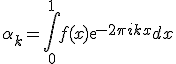
Но как правила функция задана только в некоторых точках или у нас есть возможность узнать её значения только в некотором конечном числе точек. Допустим,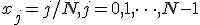 
.В этом случае аналогом функции непрерывной интерполяции функции будет дискретный вариант:
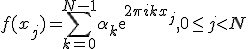
Разложение имеет место когда функцию можно приблизить тригонометрическим многочленом следующего вида в заданных нам точках
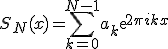
Система функций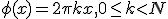 
является ортогональной, на множестве точек 
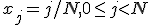при том что 
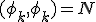, таким образом разложение имеет место и коэффициенты 
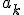представляются в виде:
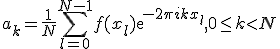
Далее для удобства записи будем использовать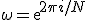 
Часто используется следующий вид формул:
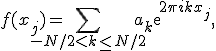и это соответствует интерполяции тригонометрическим многочленом
,
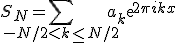где коэффициенты 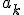считаются по тем же формулам.
Если вычисления проводить по вышеприведённым формулам, то на выполнения каждого из преобразований потребуется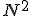 
арифметических операций (считаем, что 
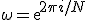уже вычислены). Если N не является простым числом, то количество операций можно значительно сократить, используя быстрое преобразование Фурье.
