Пример использования

Рассмотрим применение тригонометрической интерполяции. Будем использовать для приближения следующий тригонометрический полином:

Будем искать приближение функции f(x). Пусть известно значения 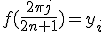при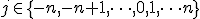

Тогда по формулам изложенным выше можно получить

Если интерполировать тригонометические функции и выбирать правильное число узлов, то погрешность приближается к нулю. Интересно рассмотреть функции, не являющиеся тригонометрическими, но обладающие периодом. Рассмотрим ряд вычислений приближенных функций с помощью программы, использующей выше изложенный алгоритм апроксимации. На вход подается функция и количество точек на промежутке 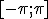, точки по умолчанию расположены равномерно на промежутке. Как будет показано ниже, это соответсвует наилучшей аппроксимации.

1. Линейная регрессия.

Линейная регрессия — метод восстановления зависимости между двумя переменными. Ниже приведен пример программы, которая строит линейную модель зависимости по заданной выборке и показывает результат на графике.

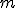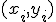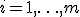Для заданного множества из пар , , значений свободной и зависимой переменной требуется построить зависимость. Назначена линейная модель

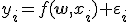
c аддитивной случайной величиной . Переменные 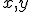принимают значения на числовой прямой 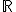. Предполагается, что случайная величина распределена нормально с нулевым матожиданием и фиксированной дисперсией 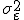, которая не зависит от переменных 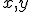. При таких предположениях параметры 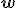регрессионной модели вычисляются с помощью метода наименьших квадратов.

Например, требуется построить зависимость цены нарезного хлеба от времени. (См. рис. далее по тексту). В таблице регрессионной выборкипервая колонка — зависимая переменная 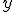(цена батона хлеба), вторая — свободная переменная 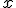(время). Всего данные содержат 195 пар значений переменных. Данные нормированы.

1. Аппроксимация функций по методу наименьших квадратов.

Если набор экспериментальных данных получен со значительной погрешностью, то интерполяция не только не требуется, но и нежелательна! Здесь требуется построить кривую, которая воспроизводила бы график исходной экспериментальной закономерности, т.е. была бы максимально близка к экспериментальным точкам, но в то же время была бы нечувствительна к случайным отклонениям измеряемой величины.

Введем непрерывную функцию φ(x) для аппроксимации дискретной зависимости f(x_i), i = 0… n. Будем считать, что φ(x) построена по условию наилучшего квадратичного приближения, если

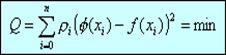. (1)

Весу ρ для i -й точки придают смысл точности измерения данного значения: чем больше ρ, тем ближе аппроксимирующая кривая «притягивается» к данной точке. В дальнейшем будем по умолчанию полагать ρ = 1 для всех точек.

Рассмотрим случай линейной аппроксимации:

φ(x) = c₀φ₀(x) + c₁φ₁(x) + … + c_mφ_m(x), (2)

где φ₀…φ_m – произвольные базисные функции, c₀…c_m – неизвестные коэффициенты, m < n. Если число коэффициентов аппроксимации взять равным числу узлов, то среднеквадратичная аппроксимация совпадет с интерполяцией Лагранжа, при этом, если не учитывать вычислительную погрешность, Q = 0.

Если известна экспериментальная (исходная) погрешность данных ξ, то выбор числа коэффициентов, то есть величины m, определяется условием:

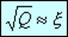(3)

Иными словами, если 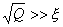, число коэффициентов аппроксимации недостаточно для правильного воспроизведения графика экспериментальной зависимости. Если 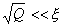, многие коэффициенты в (2) не будут иметь физического смысла.

Для решения задачи линейной аппроксимации в общем случае следует найти условия минимума суммы квадратов отклонений для (2). Задачу на поиск минимума можно свести к задаче поиска корня системы уравнений 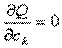, k = 0… m. (4).

Подстановка (2) в (1), а затем расчет (4) приведет в итоге к следующей системе линейных алгебраических уравнений:

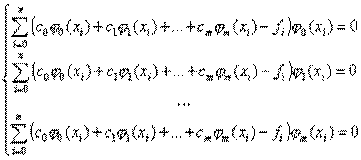
Далее следует решить полученную СЛАУ относительно коэффициентов c₀…c_m. Для решения СЛАУ обычно составляется расширенная матрица коэффициентов, которую называют матрицей Грама, элементами которой являются скалярные произведения базисных функций и столбец свободных коэффициентов:

,

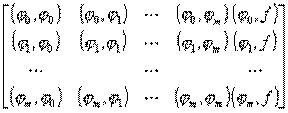где 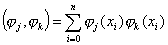, , 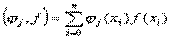j = 0… m, k = 0… m.

После того как с помощью, например, метода Гаусса найдены коэффициенты c₀…c_m, можно построить аппроксимирующую кривую или вычислить координаты заданной точки. Таким образом, задача аппроксимации решена.