Выбор формы уравнения регрессии. y – результирующий признак (зависимая переменная)

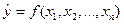
y – результирующий признак (зависимая переменная)

x₁, x₂, …, x_n – факторы (независимые переменные)

Для построения уравнения множественной регрессии используются следующие функции:

1. Линейная:

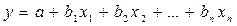
Для построения используют Анализ данных 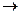Регрессия.

1. Степенная:
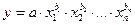
2. Экспоненциальная:
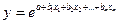
3. Гиперболическая:
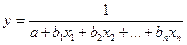
4. Логарифмическая:

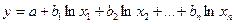
Для построения используют МНК.

; ; …;

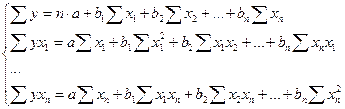
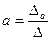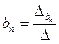
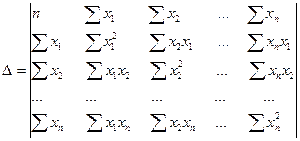
Другой вид уравнения множественной регрессии – это уравнение регрессии в стандартизированном масштабе.

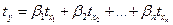
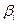- стандартизированные коэффициенты

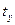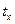, - стандартизированные переменные

,

;

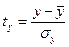
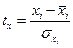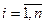
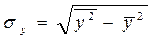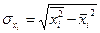
Также применим МНК.

Связь коэффициентов множественной регрессии b_i со стандартизированными коэффициентами :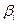

;

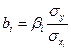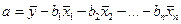
Вариация: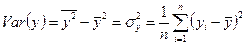

Ковариация: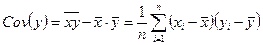

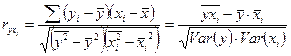
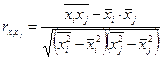
Матрицу парных коэффициентов корреляции можно найти, используя Анализ данных Корреляция.

Пример:

	y	x1	x2
y
x1	0,7
x2	-0,8	0,5

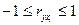
Если 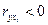, то связь обратная. Если 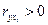, то связь прямая. Если 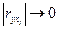, то связь слабая.

Необходимо, чтобы ,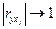

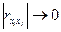
Если 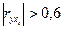, то присутствует явление мультиколлинеарности (линейная зависимость факторов). Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по определенным факторам с помощью МНК.