Линейный коэффициент парной корреляции для линейной регрессии:
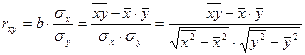 ,
, 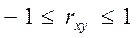
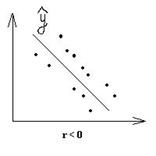
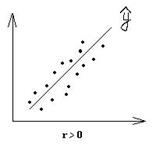
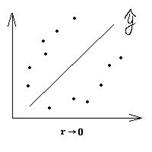
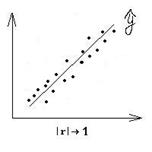
Линейный коэффициент корреляция оценивает тесноту связи рассматриваемых признаков (x, y)
Если 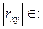
· (0,3; 0,5) - связь слабая
· (0,5; 0,7) - связь умеренная
· (0,7; 0,8) - связь достаточно тесная
· (0,8; 0,9) - связь тесная
· (0,9; 1) - связь очень тесная
Индекс корреляции для нелинейной регрессии:
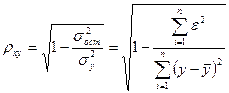 ,
, 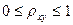
Оценка качества построенной модели дает коэффициент (индекс) детерминации и среднюю ошибку аппроксимации.
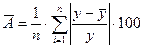
Долю дисперсии, объясняемую регрессией в общей дисперсии результативного признака (y) характеризует коэффициент детерминации:
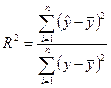 ,
, 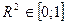
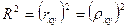
Данные формулы справедливы, если:
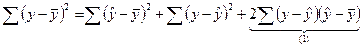 , (1)=0
, (1)=0
Если 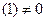 , то
, то 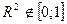
Средний коэффициент эластичности 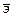 показывает на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения.
показывает на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения.
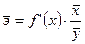 ,
, 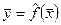
F-тест оценивает качество уравнения регрессии.
Выдвигается гипотеза H0, которая говорит о статистической незначимости уравнения регрессии и показателя тесноты связи.
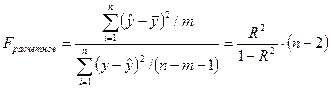
n – число уровней
m – число параметров при переменных x
Fрасчетное сравнивают с табличным значением.
Если 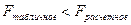 , то гипотеза отклоняется, т.е. уравнение значимо и надежно.
, то гипотеза отклоняется, т.е. уравнение значимо и надежно.
Для оценки статистической значимости коэффициентов регрессии и корреляции используют t-критерий Стьюдента и доверительные интервалы каждого из показателей.
Выдвигается гипотеза H0, которая говорит о случайно природе показателей.
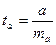 ;
; 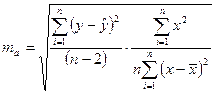 ; ma - случайная ошибка
; ma - случайная ошибка
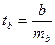 ;
; 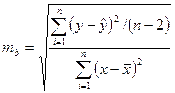 ; mb - случайная ошибка
; mb - случайная ошибка
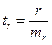 ;
; 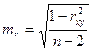 ; mr - случайная ошибка
; mr - случайная ошибка
ta, tb, tr сравнивают с табличными значениями.
Если 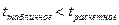 , то гипотеза отклоняется, т.е. a, b, r неслучайно отличаются от нуля и сформировались под влиянием систематических действий фактора x.
, то гипотеза отклоняется, т.е. a, b, r неслучайно отличаются от нуля и сформировались под влиянием систематических действий фактора x.
 2015-05-18
2015-05-18 293
293








