Теоретические основы

ПОСТРОЕНИЕ МОДЕЛИ

ПАРНОЙ КОРРЕЛЯЦИИ

Цель работы: получение навыков в построении и анализе парных корреляционных моделей, применяемых в управлении строительным производством.

Время выполнения работы: 4 часа.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

Методы теории корреляции позволяют определить количественную зависимость между различными техническими, технологическими, организационными и другими факторами, т.е. строить экономико-статистические модели.

Различают функциональную и корреляционную зависимости. Под функциональной понимается такая зависимость, когда с изменением одного фактора изменяется другой, одному значению независимого фактора обычно соответствует только одно значение зависимого фактора. Корреляционная зависимость - это такая зависимость, при которой изменение одной случайной величины вызывает изменение среднего значения другой. Конкретных же значений зависимого переменного, соответствующих одному значению независимого, может быть несколько. Корреляционные зависимости могут быть установлены только при обработке большого количества наблюдений. При корреляционном анализе решаются следующие задачи:

* устанавливается наличие корреляции (связи) между величинами;

* устанавливается формула линии связи (линии регрессии);

* определяются параметры линии регрессии;

* определяются значимость установленной зависимости и достоверность отдельных параметров.

Наличие корреляции приближенно может быть определено путем визуального анализа поля корреляции. Корреляционным полем называют нанесенные на график в определенном масштабе точки, соответствующие одновременным значениям двух величин.

Тесноту связи между двумя величинами можно определить визуально по соотношению короткой и продольной осей эллипса рассеяния наблюдений, нанесенных на поле корреляции. Чем больше отношение продольной стороны к короткой, тем связь теснее.

Более точно теснота связи характеризуется коэффициентом корреляции r. Коэффициент корреляции лежит в пределах 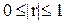. В случае, если r=0, то линейной связи нет. Если |r|=1, то между двумя величинами существует функциональная связь. При положительном r наблюдается прямая связь, т.е. с увеличением независимого переменного увеличивается зависимое. При отрицательном коэффициенте наблюдается обратная связь - с увеличением независимого переменного зависимое переменное уменьшается.

Коэффициент корреляции определяется по формуле

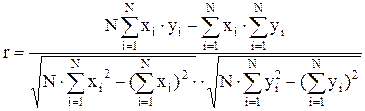, (3.1)

где x и y -текущие значения наблюдаемых величин; N - число наблюдений.

Для численного выражения параметров линии регрессии, выражающих связь между двумя величинами, обычно применяется метод наименьших квадратов. Сущность этого метода состоит в том, что выбирается такая линия, при которой сумма квадратов разностей между фактическими наблюдениями зависимой переменной и расчетными значениями, полученными по регрессионной формуле, минимальна

S= ,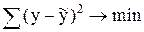

где 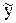- расчетное значение зависимого переменного по регерессивной формуле.

Допустим, 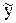=а+bx. Тогда

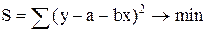
Возьмем частные производные по a и по b и приравняем их к нулю:

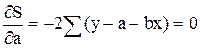
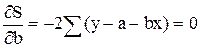
Полученную систему обычно преобразуют

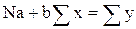
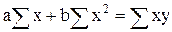
Решив систему относительно b и a, получим формулы

,

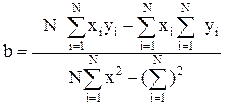a= 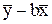. (3.2)

При линейной корреляции коэффициент корреляции r является не только критерием тесноты связи, но и критерием точности аппроксимации (подбора формулы, выражающей зависимость).

Далеко не всегда данные статистических наблюдений модно аппроксимировать в виде линейной зависимости. Очень часто оказывается, что линейная зависимость не дает необходимой тесноты связи. В этом случае аппроксимацию проводят с помощью зависимостей, отличных от линейной. С этой целью чаще всего используются

* степенная;

* логарифмическая;

* параболическая;

* многочлен степени n;

* зависимости периодического вида.

Для определения параметров нелинейной зависимости пользуются процедурой метода наименьших квадратов, но предварительно проводят линеаризацию. С этой целью, как правило, производят логарифмирование, например, зависимость степенного вида представляется аналитической формулой

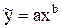, (3.3)

которая после логарифмирования будет представлена в виде

,

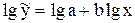параметры lga и b находятся по методу наименьших квадратов по формуле

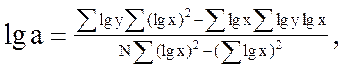
(3.4)

b= .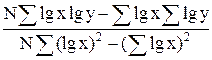

Аналогично можно получить выражение для параметров остальных типов кривых.

Логарифмическая зависимость выражается формулой вида:

.

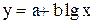Расчетные формулы для определения параметров а и в имеют вид:

,

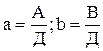где

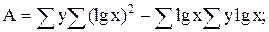
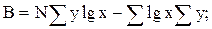
Д=N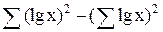

В виде параболы второго порядка зависимость выражается формулой

y =a + bx +cx .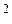

Если степень независимого переменного равна трем, то эта парабола третьего порядка и т.д. Линейная зависимость также является частным случаем многочлена.

Аппроксимация (определение параметров) параболической кривой осуществляется методом наименьших квадратов. В целевую функцию метода наименьших квадратов 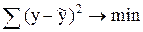вместо расчетных значений у подставим правую часть уравнения:

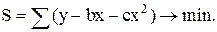
Возьмем частные производные от этого выражения по а, b и с:

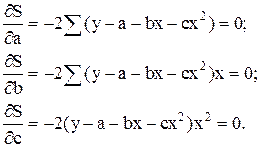
Получим систему нормальных или ортогональных уравнений, которая после несложных преобразований примет вид:

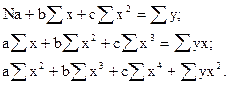
Решая систему любым известным методом, находим параметры параболы а,b и с.

Параметры параболы можно определить из выражений:

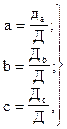
где Д - главный определитель системы линейных уравнений; Д 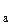-определитель системы уравнений, в котором столбец коэффициентов при а заменяют столбцом свободных членов; Д 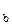- определитель системы, в котором столбец коэффициентов при b заменен столбцом свободных членов; Д 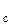- определитель системы, в котором столбец коэффициентов при «с» заменен столбцом свободных членов.

Определители матрицы можно расписать в виде следующих выражений:

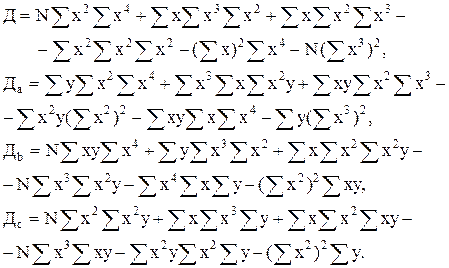
Кривые периодического вида могут найти широкое распространение при аппроксимации зависимости многих экономических явлений во времени. Например, такими кривыми выражаются влияния сезонных факторов на организацию строительства и материально-технического обеспечения. Наблюдения времени при этом можно представить в виде равноотстоящих, например, х, выраженных в радианах или градусах. Если взять период времени, равный году, и провести ежемесячные наблюдения какого-либо экономического показателя, то время как аргумент может быть записан в виде

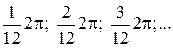
В течение года можно получить 12 наблюдений экономического показателя 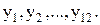Тогда зависимость величины «y» от времени можно выразить уравнением

,

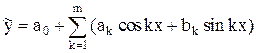где k=1,2,3...,m - заданное число гармоник многочлена;

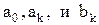- коэффициенты линии регрессии, общим числом 2m+1.

Если N>2m+1, то коэффициенты 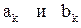находятся по методу наименьших квадратов, который дает следующие выражения для коэффициентов линии регрессии:

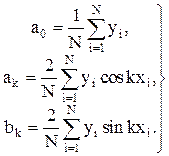
Оценка точности аппроксимации криволинейной зависимостью производится при помощи корреляционного отношения:

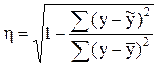(3.5)

Корреляционное значение всегда 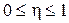, оно всегда положительно. Если 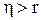, то кривая точнее аппроксимирует зависимость, чем прямая; для прямой r= .

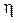Дополнительной оценкой точности аппроксимации, часто применяемой при оценке нелинейной корреляции, является средняя относительная ошибка аппроксимации, которая определяется по формуле

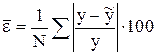. (3.6)

Коэффициент корреляции r, рассчитанный по выборочным данным, может не совпасть с истинным коэффициентом корреляции, соответствующим генеральной совокупности .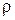

Среднеквадратичное отклонение приближенно определяется по формуле

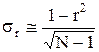. (3.7)

При больших выборках можно предположить, что коэффициент корреляции распределен по нормальному закону, тогда можно утверждать, что

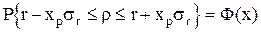
Особенно интересна проверка так называемой нулевой гипотезы. Известно, что если коэффициент корреляции по модулю больше 0, то между двумя случайными величинами имеется связь. Однако r, определенный по частичной выборке, отличается от истинного коэффициента корреляции 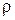. Может быть, что при |r|>0, 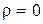, тогда связь, установленная по частичной выборке, в генеральной совокупности, отсутствует. Для ответа на вопрос, есть ли связь в генеральной совокупности, осуществляют проверку на значимость (коэффициент корреляции существенно отличен от нуля) коэффициента корреляции. Если

|r|> 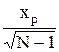(3.8)

то с заданной вероятностью Р можно утверждать, что коэффициент r сущест-

венно отличен от нуля (это означает, что нулевая гипотеза отвергается) и рассматриваемая связь в генеральной совокупности существует. Однако при малых объемах статистического материала гипотеза о нормальном распределении коэффициента корреляции, как правило, не подтверждается. При небольшом числе испытаний вопрос о значимости коэффициента корреляции рассматривается с использованием t-критерия Стьюдента. При этом определяется расчетное значение критерия по формуле

t= 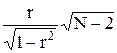(3.9)

где N-2 - число степеней свободы f.

Теоретическое значения t определяется по таблице распределения Стьюдента (прил. II). Если 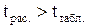при заданном уровне значимости, то предположение о нулевом значении коэффициента корреляции в генеральной совокупности не подтверждается.

При аппроксимации корреляционной зависимости полученная линия регрессии отвечает только частичной выборке, то есть тем данным, которые были использованы при статистической обработке. Для распространения этой зависимости на генеральную совокупность необходимо оценить значение коэффициентов регрессии, так как может оказаться, что при условии неравенства коэффициента регрессии нулю истинный коэффициент регрессии, отражающий генеральную совокупность, будет нулевым. В этом случае прогнозировать по полученной кривой нельзя. Значимость отдельных коэффициентов определяется при помощи t - критерия Стьюдента.

Для оценки значимости коэффициентов регрессии расчетное значение t - критерия Стьюдента определяется по формулам

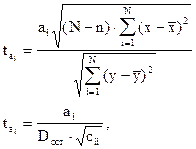(3.10)

где 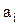- коэффициент регрессии при i - м члене уравнения регрессии;

n - число коэффициентов регрессии;

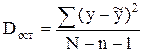- остаточная дисперсия;

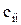- диагональный элемент обратной матрицы.

По первой формуле определяется значение t - критерия при одной переменной, а по второй формуле - при множественной корреляции.

При этом если 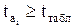, то коэффициент корреляции существенно отличен от нуля, а следовательно, этот коэффициент имеет значение отличное от нуля и в генеральной совокупности.

Оценка коэффициентов регрессии при помощи t - критерия Стьюдента применяется только для линейных корреляционных связей. Но так как при помощи метода наименьших квадратов путем линеаризации определяются линейные коэффициенты регрессии, то t - критерий может применяться также для любого вида функции в линеаризованной форме.

Значимость уравнения регрессии определяется возможностью надежно прогнозировать средние значения исследуемой величины. Уравнение прогноза получено на основе частичной совокупности, но истинная зависимость, свойственная генеральной совокупности, может существенно отличаться от полученного соотношения. Для изучения степени соответствия полученного уравнения регрессии истинному соотношению следующему из генеральной совокупности используют F - критерий Фишера, определяемый по формуле

F= 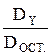(3.11)

где 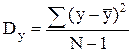- дисперсия фактических значений зависимого переменного; N-n-1= 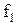; N-1= 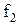- число степеней свободы.

По числу степеней свободы, задавшись вероятностью, можно определить табличное значение критерия Фишера, значения для которых приведены в прил. III. Если F 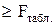, то уравнение регрессии считается значимым, т.е. уравнение будет давать достаточно надежные прогнозы и может быть использовано.

Уравнение регрессии из-за вероятностного характера имеет некоторую случайную компоненту h, на величину которой могут отличаться значения зависимой переменной от ее истинных значений

Величина «h» отражает влияние неучтенных факторов и несоответствие частичной совокупности, по которой определялось уравнения регрессии генеральной совокупности. Для надежного прогнозирования необходимо определить доверительный интервал исследуемой величины y.

Если предположить, что величина h является случайной величиной, распределенной по нормальному закону, то истинное значение случайной величины «y» будет находиться в интервале

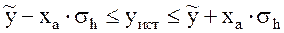
где ;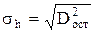

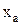- аргумент, характеризующий вероятность попадания случайной величины в заданные пределы; определяется из прил.II.

ПРИМЕР

Рассмотрим зависимость выработки, приходящейся на одного рабочего от коэффициента текучести кадров. Статистические данные приведены в табл. 3.1.

Таблица 3.1.

Наблюдение i	Результативный признак y	Фактор x	Наблюдение i	Результативный признак y	Фактор x
	10,3	0,15		5,3	0,26
	9,6	0,18		5,8	0,23
	8,9	0,19			0,37
	4,7	0,44		5,1	0,57
	6,3	0,35		4,3	0,37
	5,4	0,28		4,6	0,28
	6,5	0,23		6,3	0,24
	5,1	0,36		7,7	0,28
	6,2	0,42			0,26

Нанесем все имеющиеся статистические данные в системе координат, по-

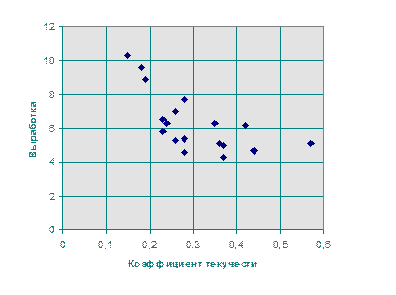
Рис. 3.1.

лучив, таким образом, поле корреляций.

Анализируя поле корреляций, задаемся гипотезой о существовании между рассматриваемыми величинами линейной зависимости вида y=a+bx. Для вычисления коэффициентов регрессии по формулам (3.2) предварительно вычислим величины:

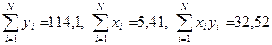
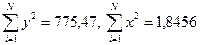
тогда коэффициенты a и b находятся из следующих выражений:

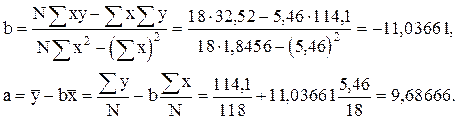
Таким образом, линейная зависимость будет описываться зависимостью вида

y=9,68666-11,03661x.

Находим коэффициент корреляции между изучаемыми величинами формуле (3.1):

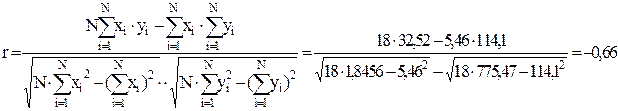
Знак минус у коэффициента корреляции показывает на обратно пропорциональную связь между изучаемыми величинами.

Оценим значимость полученного коэффициента корреляции, проверив справедливость нулевой гипотезы по формуле (3.8), получаем

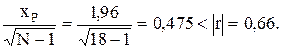
Таким образом, нулевая гипотеза не подтвердилась и связь между рассматриваемыми величинами существует.

Проведем проверку значимости коэффициентов регрессии, используя формулу (3.10), и получим для коэффициентов a и b соответственно следующие значения

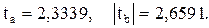
Находим табличное значение критерия Стьюдента по приложению II. Для вероятности 5 % и числе степеней свободы f=N-2=16 (число наблюдений минус число коэффициентов уравнения регрессии) t=2,12, а с вероятностью 2 % - t=2,567. Таким образом, полученные результаты свидетельствуют о том, что коэффициенты линейного уравнения регрессии a и b с вероятностью 95 % будут отличны от нуля (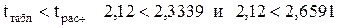). Если же требуется повышенная степень вероятности (это характерно для особо ответственных расчетов), то полученная модель не отвечает этим требованиям, так как гипотеза об отличии коэффициентов регрессии от нуля не подтвердилась, то есть 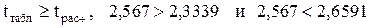, и, следовательно, с вероятностью 2 % коэффициент «a»уравнения регрессии будет равняться нулю.

Найдем оценку значимости уравнения регрессии с помощью критерия Фишера. С этой целью определим по формуле (3.11) значение критерия 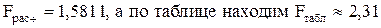для степеней свободы 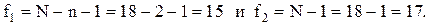Таким образом, 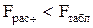. Следовательно, гипотеза о значимости уравнения регрессии не подтверждается, а это означает, что предсказательная сила среднего значения изучаемой величины выше, чем у полученного уравнения регрессии.

Анализируя все полученные оценки, можно сделать вывод о том, что использование линейной аппроксимации при решении поставленной задачи не оправдано.

Рассмотрим аппроксимацию изучаемых величин при помощи степенной зависимости вида 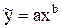. Коэффициенты уравнения регрессии «a» и «b» находятся по формулам (3.4) и принимают значения a=3,04 b=-0,56, таким образом,

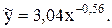
Тесноту связи оценим по корреляционному соотношению, задаваемому формулой (3.5). Это соотношение принимает значение 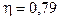, которое является больше коэффициента корреляции, следовательно, степенная зависимость описывает изучаемое явление лучше, чем прямолинейная. А средняя относительная ошибка аппроксимации, подсчитанная по формуле (3.6), равна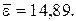

Оценим значимость полученного коэффициента корреляции, проверив справедливость нулевой гипотезы по формуле (3.8).

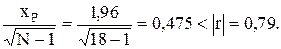
Таким образом, нулевая гипотеза не подтвердилась и связь между рассматриваемыми величинами существует.

Проведем проверку значимости коэффициентов регрессии, используя формулу (3.10). Как известно, эта формула справедлива только для линейных соотношений, поэтому для ее использования осуществим предварительную линеаризацию уравнения, в результате получим

.

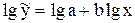Применяя к этому линеаризованному соотношению формулу (3.10), получим

.

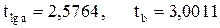Находим табличное значение критерия Стьюдента по прил. II. При вероятности 5 % и числе степеней свободы f=N-2=16 (число наблюдений минус число коэффициентов уравнения регрессии) t=2,12, а с вероятностью 2 % - t=2,567. Таким образом, полученные результаты свидетельствуют о том, что коэффициенты степенного уравнения регрессии a и b с вероятностью 95 % будут отличны от нуля (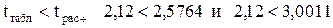). Полученная модель и при повышенном значении вероятности (98 %) сохраняет значимость коэффициентов регрессии 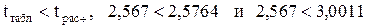и, следовательно, является более предпочтительной по сравнению с линейной.

Найдем оценку значимости уравнения регрессии с помощью критерия Фишера. С этой целью определим по формуле (3.11) значение критерия 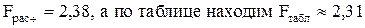для степеней свободы 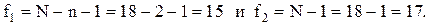Таким образом, 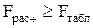. Следовательно, гипотеза о значимости уравнения регрессии подтверждается, а это означает, что предсказательная сила среднего значения изучаемой величины ниже, чем у полученного уравнения регрессии.