Цель: По опытным данным построить уравнение регрессии вида 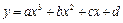 .
.
ПРИМЕР. Рассмотрим решение задачи на примере опытных данных
| Х | ||||||||||||
| Y |
Введем эти данные в электронную таблицу вместе с подписями в ячейки А1-М2. Построим график. Для этого обведем данные Y (ячейки В2-М2), вызываем мастер диаграмм, выбираем тип диаграммы «График», вид диаграммы – график с точками (второй сверху левый), нажимаем «Далее», переходим на закладку «Ряд» и в поле «Подписи оси Х» делаем ссылку на В2-М2, нажимаем «Готово». Видно, что график имеет 2 экстремума и один перегиб, поэтому его можно приблизить полиномом 3 степени 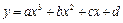 . Для нахождения коэффициентов
. Для нахождения коэффициентов 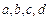 нужно решить систему уравнений:
нужно решить систему уравнений:
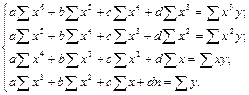
Рассчитаем суммы. Для этого в ячейку А3 вводим подпись «X^2», а в В3 вводим формулу «=В1*В1» и автозаполнением переносим ее на всю строку В3-М3. В ячейку А4 вводим подпись «X^3», а в В4 формулу «=В1*В3» и автозаполнением переносим ее на всю строку В4-М4. В ячейку А5 вводим «X^4», а в В5 формулу «=В4*В1», автозаполняем строку. В ячейку А6 вводим «X^5», а в В6 формулу «=В5*В1», автозаполняем строку. В ячейку А7 вводим «X^6», а в В7 формулу «=В6*В1», автозаполняем строку. В ячейку А8 вводим «X*Y», а в В8 формулу «=В2*В1», автозаполняем строку. В ячейку А9 вводим «X^2*Y», а в В9 формулу «=В3*В2», автозаполняем строку. В ячейку А10 вводим «X^3*Y», а в В10 формулу «=В4*В2», автозаполняем строку. Теперь считаем суммы. Выделяем другим цветом столбец N, щелкнув по заголовку и выбрав цвет. В ячейку N1 помещаем курсор и щелкнув по кнопке автосуммы со значком S, вычисляем сумму первой строки. Автозаполнением переносим формулу на ячейки N1-N10.
Решаем теперь систему уравнений. Для этого вводим основную матрицу системы. В ячейку А13 вводим подпись «А=», а в ячейки матрицы В13-Е16 вводим ссылки, отраженные в таблице
| В | С | D | Е | |
| 13 | =N7 | =N6 | =N5 | =N4 |
| 14 | =N6 | =N5 | =N4 | =N3 |
| 15 | =N5 | =N4 | =N3 | =N1 |
| 16 | =N4 | =N3 | =N1 |
Вводим также правые части системы уравнений. В G13 вводим подпись «В=», а в Н13-Н16 вводим, соответственно ссылки на ячейки «=N10», «=N9», «=N8», «=N2». Решаем систему матричным методом. Из высшей математики известно, что решение равно 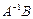 . Находим обратную матрицу. Для этого в ячейку I13 вводим подпись «А обр.» и, поставив курсор в J13 задаем формулу МОБР (категория «Математические»). В качестве аргумента «Массив» даем ссылку на ячейки B13:E16. Результатом также должна быть матрица размером 4х4. Для ее получения обводим ячейки J13-M16 мышью, выделяя их и нажимаем F2 и Ctrl+Shift+Enter. Результат – матрица
. Находим обратную матрицу. Для этого в ячейку I13 вводим подпись «А обр.» и, поставив курсор в J13 задаем формулу МОБР (категория «Математические»). В качестве аргумента «Массив» даем ссылку на ячейки B13:E16. Результатом также должна быть матрица размером 4х4. Для ее получения обводим ячейки J13-M16 мышью, выделяя их и нажимаем F2 и Ctrl+Shift+Enter. Результат – матрица 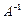 . Найдем теперь произведение этой матрицы на Столбец В (ячейки Н13-Н16). Вводим в ячейку А18 подпись «Коэффициенты» и в В18 задаем функцию МУМНОЖ (категория – «Математические»). Аргументами функции «Массив 1» служит ссылка на матрицу
. Найдем теперь произведение этой матрицы на Столбец В (ячейки Н13-Н16). Вводим в ячейку А18 подпись «Коэффициенты» и в В18 задаем функцию МУМНОЖ (категория – «Математические»). Аргументами функции «Массив 1» служит ссылка на матрицу 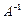 (ячейки J13-M16), а в поле «Массив 2»даем ссылку на столбец В (ячейки H13-H16). Далее выделяем В18-В21 и нажимаем F2 и Ctrl+Shift+Enter. Получившийся массив – коэффициенты уравнения регрессии
(ячейки J13-M16), а в поле «Массив 2»даем ссылку на столбец В (ячейки H13-H16). Далее выделяем В18-В21 и нажимаем F2 и Ctrl+Shift+Enter. Получившийся массив – коэффициенты уравнения регрессии 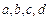 . В результате получаем уравнение регрессии вида:
. В результате получаем уравнение регрессии вида:
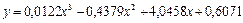 .
.
Построим графики исходных данных и полученных на основании уравнения регрессии. Для этого в ячейку А11 вводим подпись «Регрессия» и в В11 вводим формулу «=$B$18*B4+$B$19*B3+$B$20*B1+$B$21». Автозаполнением, переносим формулу в ячейки В11-М11. Для построения графика выделяем ячейки В11-М11 и, удерживая клавишу Ctrl, выделяем также ячейки В2-М2. Вызываем мастер диаграмм, выбираем тип диаграммы «График», вид диаграммы – график с точками (второй сверху левый), нажимаем «Далее», переходим на закладку «Ряд» и в поле «Подписи оси Х» делаем ссылку на В2-М2, нажимаем «Готово». Видно, что кривые почти совпадают.
Задание на самостоятельную работу
Рассматривается зависимость урожайности некоторой культуры yi от количества внесенных в почву минеральных удобрений xi. Предполагается, что эта зависимость квадратичная. Необходимо найти уравнение регрессии вида 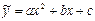 .
.
| Вари-ант | Внесено удобрений хi, ц./га (одинаковое для всех вариантов) | |||||||||
| Урожайность yi (по вариантам) | ||||||||||
| 1. | 19,4 | 28,8 | 48,2 | 58,0 | 80,3 | 88,7 | 96,1 | 119,2 | 146,9 | 168,0 |
| 2. | 26,6 | 45,7 | 63,8 | 78,3 | 86,4 | 97,7 | 96,9 | 113,6 | 113,6 | 120,9 |
| 3. | 13,1 | 27,2 | 36,9 | 47,3 | 56,2 | 68,0 | 77,4 | 74,6 | 79,4 | 79,9 |
| 4. | 25,2 | 46,2 | 56,7 | 77,6 | 91,5 | 112,3 | 106,2 | 131,9 | 149,4 | 141,8 |
| 5. | 29,8 | 58,8 | 72,2 | 101,5 | 141,0 | 135,1 | 156,6 | 181,7 | 216,6 | 208,2 |
| 6. | 17,8 | 27,4 | 32,0 | 43,7 | 44,5 | 41,4 | 34,4 | 36,9 | 25,1 | 15,1 |
| 7. | 12,7 | 20,0 | 24,9 | 21,5 | 21,3 | 20,4 | 13,4 | 13,1 | 4,0 | 2,8 |
| 8. | 26,2 | 44,3 | 66,7 | 72,5 | 89,5 | 97,5 | 98,0 | 117,5 | 97,2 | 108,2 |
| 9. | 29,5 | 54,7 | 67,5 | 97,4 | 102,8 | 118,2 | 131,7 | 128,7 | 134,5 | 133,0 |
| 10. | 15,5 | 25,4 | 36,4 | 39,9 | 43,3 | 38,8 | 49,1 | 52,6 | 51,0 | 43,2 |
| 11. | 23,5 | 44,9 | 47,1 | 70,2 | 94,4 | 104,5 | 125,9 | 126,6 | 159,3 | 180,8 |
| 12. | 9,8 | 15,0 | 23,8 | 22,0 | 20,6 | 13,3 | 7,1 | 4,6 | 2,7 | 1,9 |
| 13. | 28,5 | 44,6 | 80,9 | 92,8 | 104,0 | 119,2 | 145,4 | 154,4 | 171,5 | 181,5 |
| 14. | 21,6 | 38,2 | 49,1 | 54,8 | 63,6 | 59,8 | 56,5 | 72,5 | 60,8 | 57,7 |
| 15. | 26,3 | 45,8 | 67,7 | 93,7 | 105,1 | 119,5 | 136,2 | 150,0 | 146,2 | 140,9 |
 2015-05-18
2015-05-18 428
428








