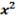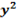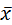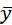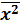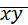От коэффициента массовости производства

Таблица 4.4.1

Данные для анализа

∑x=

∑y=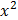

∑

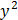∑ xy =

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов:

;

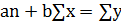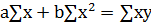где n – объём исследуемой совокупности (n =10).

Отсюда b= , .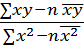

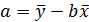Расчет линейного коэффициента корреляции:

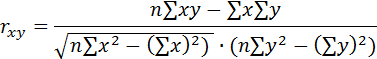Расчет стандартного отклонения уравнения регрессии:

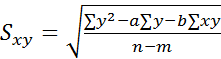где m – число параметров в уравнении (в нашем случае m =2); n – объём исследуемой совокупности (n =10).

Отобразим все расчеты в таблице 4.4.2.

Таблица 4.4.2

Данные для построения регрессионной зависимости

b	a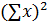

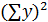
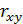
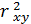
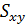
Уравнение регрессии:

y =??? x –(+)???.

Коэффициент детерминации

=??????,

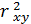что свидетельствует о сильной (слабой) связи между признаками x и y.

Рис.4. График зависимости себестоимости незавершённого производства

от коэффициента массовости производства

Сопоставим найденную величину со средним значением результативного признака:

=?? %,

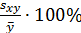что говорит о сильной (слабой) вариации результативного признака y.