Нелинейные регрессионные модели и их классификация

Нелинейные регрессионные модели — модели вида

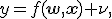
которые не могут быть представлены в виде скалярного произведения

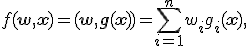
где 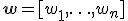— параметры регрессионной модели, 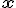— свободная переменная из пространства 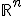, 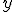— зависимая переменная, 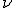— случайная величина и 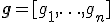— функция из некоторого заданного множества.

Значения параметров в случае нелинейной регрессии находят с помощью одного из методов градиентного спуска, например алгоритма Левенберга-Марквардта.

Нелинейная модель. уравнение зависимости между Уи Х может быть представлено степенной функцией У от Х, 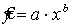, показательной 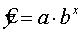, гиперболической 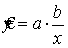и д. р.

Для оценки параметров в этих случаях метод наименьших квадратов можно применять после логарифмирования, либо после введения новой переменной.

Для показательной функции:

ln y=ln a+x ln b

Y α β

Y = α + х β Þ а = еα; b=еβ

Для степенной функции

ln y=ln a+b ln x

Y α X

Y = α + β X

Для гиперболической функции

у=а+b/x

1/х=Х

У=а+bХ