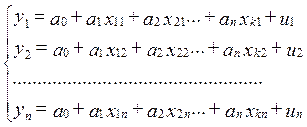2015-05-18
762
Модель множественной регрессии имеет вид:
Согласно методу наименьших квадратов, необходимо найти такие значения оценок параметров модели, которые соответствуют минимуму суммы квадратов остатков.
алгоритм:
1. Заполнить таблицу: Записываем в столбцы значения переменных.
| A | B | |||
| y1 | x11 | … | xk1 | |
| y2 | x12 | … | xk2 | |
| … | … | … | … | … |
| n | yn | x1n | … | xkn |
| n+1 | ||||
| n+2 | ||||
| n+3 | ||||
| n+4 | ||||
| n+5 |
2. Выделяем данный диапазон и нажимаем Данные/ Анализ данных/ Корреляция
3. В результате будет получена матрица коэффициентов парной корреляции
| y | x1 | x2 | x3 | |
| y | ||||
| x1 | ||||
| x2 | ||||
| x3 | ||||
4. на основании полученных данных делаем вывод о параметрах модели, определяем характер линейной связи. Выбираем наиболее коллерируемые переменные.
