Имитационное моделирование

Метод Монте-Карло. При разработке и экспертизе инвестици­онного проекта вопрос о его эффективности решается на основе анализа значений различных интегральных показателей — NPV, IRR, РВ, PI и т.д. Но все расчеты проводятся для базового варианта инвестиционного проекта, реализация которого, по мнению разра­ботчиков, наиболее правдоподобна. В данной ситуации строится только одна модель прогнозных потоков денежных средств. И эта модель является моделью принятия решений в условиях определен­ности.

Предпосылка полной определенности приводит к значительно­му упрощению действительности при моделировании. На практике нельзя быть полностью уверенным, что при реализации инвестици­онного проекта все денежные потоки будут в точности соответство­вать прогнозным. Наоборот, с момента реализации проекта на каж­дом этапе будет возникать все большее расхождение между про­гнозными и реальными денежными потоками. Может даже возник­нуть ситуация, когда задержки в оплате продукции, рост цен на импортные материалы в связи с изменением валютного курса, из­менение налоговых ставок или другие негативные события приведут к полному краху проекта или, как минимум, к существенным до­полнительным издержкам. Как оценить устойчивость проекта к из­менениям внешней среды? Как количественно измерить риск, свя­занный со всем проектом в целом? Применение имитационного моделирования методом Монте-Карло в инвестиционных расчетах позволяет дать ответы на эти вопросы.

Проведение риск-анализа методом Монте-Карло не исключает осуществления на предыдущем этапе стандартных инвестиционных расчетов. Этот метод скорее является инструментом, который улучшает их результаты. Наличие хорошей исходной модели инве­стиционного проекта — необходимая база для проведения значимо­го, результативного имитационного моделирования. Результаты срав­нительного анализа стандартных инвестиционных расчетов и прове­дения анализа риска методом Монте-Карло приведены в табл. 5.

Таблица 5. Стандартные инвестиционные расчеты и риск-анализ методом Монте-Карло Характери­ стика Стандартные расчеты Риск-анализ Метод Монте-Карло Переменные Детерминированные (значе­ния точно определены) Случайные величины с заданными законами рас­пределения Модель Модель денежных потоков Модель денежных потоков Процесс Расчет одного прогнозного варианта (сценария) реали­зации проекта Расчет множества случай­ных вариантов (сценариев) реализации проекта Результат Единственное значение ин­тегрального показателя эф­фективности проекта Распределение вероятно­стей интегрального показа­теля эффективности проек­та

Метод Монте-Карло, будучи одним из наиболее сложных мето­дов количественного анализа рисков, преодолевает недостатки ана­лиза чувствительности и анализа сценариев. Оба этих метода пока­зывают воздействие определенного изменения одной или несколь­ких переменных на показатель эффективности (например, NPV^[1]). Основные недостатки этих методов и способы их устранения с по­мощью метода Монте-Карло указаны в табл. 6.

Таблица 6. Недостатки анализа чувствительности и сценариев и метод Монте-Карло Метод Недостаток Решение с помощью имитационного моделирования Анализ чувстви­ тельности Не учитывается наличие корреляции между состав­ляющими проекта Корреляция моделируется раз­ными методами и учитывается в модели   Рассматривается влияние только одной варьируемой переменной при неизмен­ных остальных составляю­щих проекта Появляется возможность одно­временно моделировать слу­чайные изменения нескольких составляющих проекта с учетом условий коррелированности Анализ сценариев Требуется отбор и анали­тическая обработка ин­формации для создания нескольких сценариев Сценарии случайны и форми­руются автоматически при реализации алгоритма метода Монте-Карло   Границы сценариев размы­ты, а построенные оценки значений переменных для каждого сценария в неко­торой степени произвольны Сценарии формируются исхо­дя из диапазонов возможных изменений случайных величин и подобранных законов рас­пределения   Рассматривается эффект ограниченного числа воз­можных комбинаций пе­ременных; рост числа сце­нариев и числа изменяе­мых переменных усложня­ет моделирование Число случайных сценариев может быть сколь угодно ве­лико, так как процесс имита­ции реализован в виде компь­ютерной программы, сущест­вует метод выбора необходи­мого числа сценариев, гаран­тирующего с определенной вероятностью (надежностью) точность результатов модели­рования

В общем случае при ослаблении предпосылки детерминирован­ности и введении предпосылки условий неопределенности в анали­зе начинают принимать участие недетерминированные переменные, характер неопределенности которых может быть разный. Так, применительно к анализу проектов рассматриваются такие виды неопределенности, как вероятностная, интервальная, интервально-­вероятностная, проекты с нечетким эффектом и с эффектом, наде­ленным правдоподобием. Применение метода Монте-Карло осно­вывается на отказе от детерминированности через введение в каче­стве исходных данных случайных величин, т.е. на наличии вероят­ностной неопределенности.

Схема реализации метода Монте-Карло в инвестиционных расче­тах. В общем случае методом Монте-Карло называют численный метод решения математических задач при помощи моделирования случайных величин.

Теоретическое описание метода появилось в 1949 г. в статье «The Monte Carlo Method»^[2]. Его создателями считают американских математиков Дж. Неймана и С. Улама. Название методу дал извест­ный своими казино город Монте-Карло в Княжестве Монако, так как именно рулетка является простейшим механическим прибором, реализующим процесс получения случайных чисел, используемый в данном математическом методе. Область применения метода Мон- те-Карло достаточно широка. В качестве примеров можно привести расчет систем массового обслуживания, расчет качества и надежно­сти изделий, вычисление определенного интеграла и др.

Схема использования метода Монте-Карло в количественном анализе рисков такова. Строится математическая модель результи­рующего показателя (характеризующего инвестиционный проект) как функции переменных и параметров. Переменными считаются случайные составляющие проекта, параметрами — те составляющие проекта, значения которых предполагаются детерминированными. Математическая модель пересчитывается при каждом новом имита­ционном эксперименте, в течение которого значения основных не­определенных переменных выбираются случайным образом на ос­нове генерирования случайных чисел. Результаты всех имитацион­ных экспериментов объединяются в выборку и анализируются с помощью статистических методов для получения распределения вероятностей результирующего показателя и расчета основных из­мерителей риска проекта.

Применение метода Монте-Карло в инвестиционных расчетах требует создания специального программного обеспечения^[3].

Разработка компьютерного обеспечения необходима по сле­дующим причинам:

• осуществляется многократное повторение имитационных экспериментов (как минимум более 100 повторений);

• используемые модели достаточно сложны (большое количе­ство переменных, учет функций распределения, условий корреля­ции и т.д.);

• обработка результатов имитации значительно упрощается;

• облегчается демонстрация метода в процессе обучения.

Метод Монте-Карло можно применить для расчета различных характеристик проекта: интегральных показателей эффективности проекта, показателей рентабельности осуществляемой в рамках проекта деятельности, исследования сетевого графика реализации проекта со случайными длительностями этапов, моделирования за­пасов продукции и материалов на складе и т.д. В дальнейшем для простоты рассматривается имитационное моделирование эффек­тивности проекта; под базовым вариантом инвестиционного проек­та понимается модель денежных потоков данного проекта (степень ее детализации зависит от желания исследователя), под результи­рующим показателем — какой-либо из интегральных показателей эффективности (например, NPV).

Процесс риск-анализа по методу Монте-Карло может быть раз­бит на этапы, 1) построения математической модели, 2) осуществ­ления имитации и 3) анализа результатов, которые далее будут рас­смотрены подробнее.

1. Построение математической модели. Первым этапом в процес­се риск-анализа является создание математической модели. Так как для проведения собственно имитационного моделирования методом Монте-Карло применяется компьютерная программа, самым глав­ным процессом в имитационном моделировании является именно формулирование модели проекта.

Для построения математической модели необходимо иметь ба­зовую модель денежных потоков инвестиционного проекта. Хотя каждый инвестиционный проект требует создания своей уникаль­ной математической модели, и ее вид — полностью продукт творче­ства разработчика, логика процедуры построения модели всегда одинакова:

• определение переменных, которые включаются в модель;

• определение типа распределения, которому эти переменные подвержены;

• определение взаимозависимостей (функциональной и веро­ятностной зависимости между переменными).

Соблюдение такой процедуры необходимо для создания модели, которая будет выглядеть следующим образом:

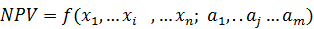(6.1)

где 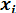— риск-переменные (составляющие денежного потока, являю­щиеся случайными величинами);

п — число риск-переменных;

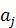— фиксированные параметры модели, т.е. те составляющие де­нежного потока, которые в результате предыдущего анализа были определены как независимые или малозависимые от внешней среды и поэтому рассматриваются как детерминиро­ванные величины;

т — число параметров модели.

Определение включаемых в модель переменных. Определение пе­ременных, которые включаются в модель, является самостоятель­ным этапом риск-анализа, отражающим прежде всего результаты исследования рисков на качественном уровне. Например, проведе­ние опросов экспертов позволяет выделить наиболее проблемные места проекта.

Решение о включении переменной в модель должно принимать­ся на основании нескольких факторов, в частности чувствительно­сти результата проекта к изменениям переменной и степени неоп­ределенности переменной (т.е. возможными границами ее измене­ния).

При формировании модели необходимо стараться выделить в качестве риск-переменных только наиболее важные, значимые пе­ременные. Причины ограничения количества риск-переменных в модели таковы:

• увеличение числа вероятностно зависимых переменных мо­дели увеличивает возможность получения противоречивых сценари­ев из-за сложности в учете и контроле зависимости и коррелируе- мости;

• с ростом числа переменных возрастают издержки (как фи­нансовые, так и временные), необходимые для корректного и акку­ратного определения их распределения вероятностей и условий ве­роятностной зависимости.

Рассмотрим основные шаги процесса определения риск-пере- менных и проиллюстрируем их на примере условного инвестици­онного проекта по производству труб.

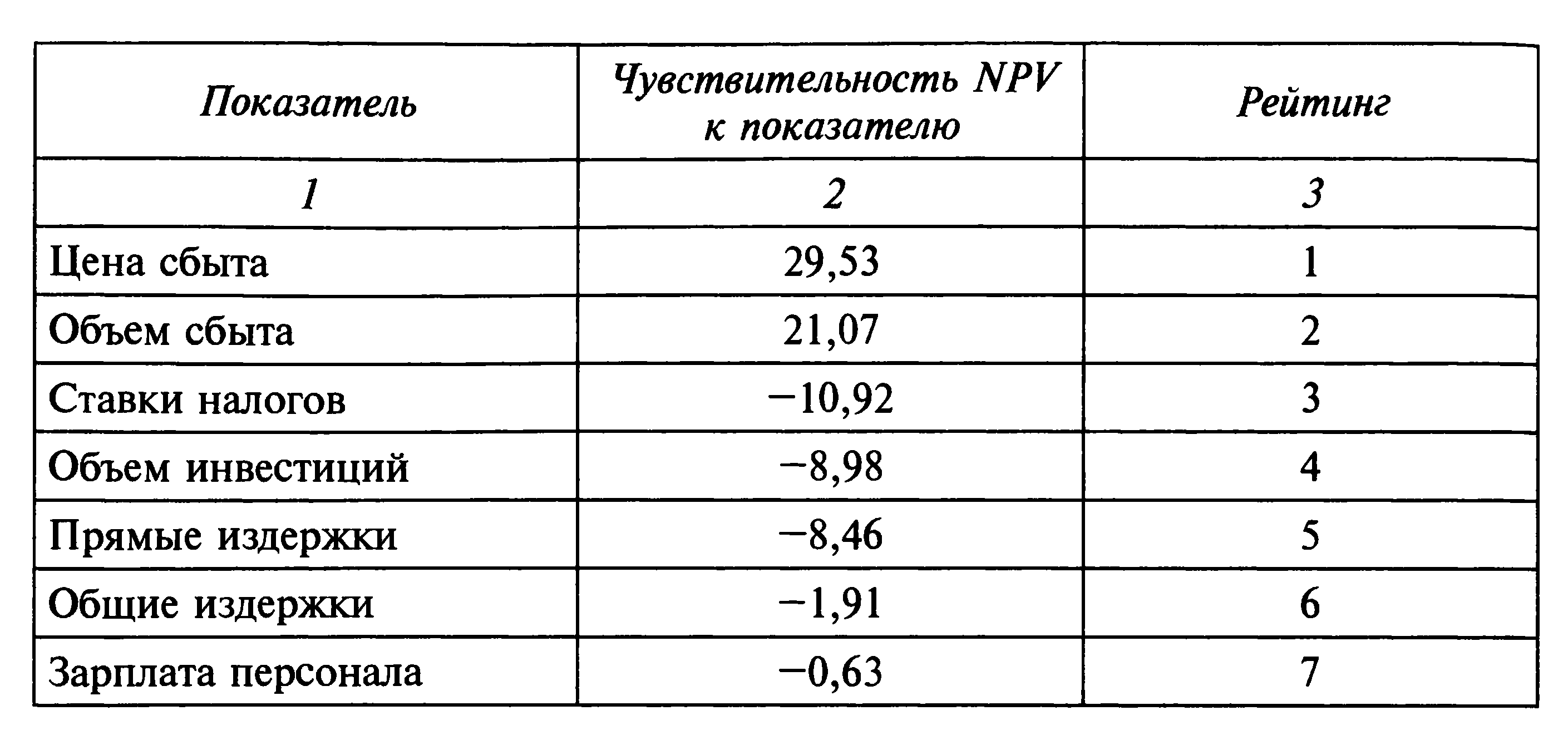
Пример. Для отбора риск-переменных по проекту производства труб были выполнены необходимые расчеты (табл. 7). Проведен анализ чувствительности результата проекта (NPV) к основным со­ставляющим элементам модели денежных потоков (гр. 1), т.е. оцен­ка того, на сколько процентов изменится NPV при изменении по­казателя на 1% (гр. 2). Полученные значения взяты по модулю и проранжированы в порядке убывания. Таким образом построен рейтинг (гр. 3).

Далее на основе рейтинга и дополнительной информации о возможных изменениях составляющих элементов модели денежных потоков выбираются риск-переменные, которые в рамках имитаци­онного моделирования будут считаться случайными величинами.

1. Выбираются переменные, оказавшиеся в верхней части рей­тинга. Для приведенного примера это могут быть, например, цена сбыта и объем сбыта, так как чувствительность NPV к ним по срав­нению с чувствительностью NPV к остальным элементам намного больше (она выше 20, а к остальным составляющим — меньше 11).

2. Анализируется экспертная информация о характере измене­ния выбранных из рейтинга переменных (колеблется сильно, слабо, детерминирована). В данном примере не имеется дополнительной информации о характере изменения переменных, поэтому оконча­тельные выводы будут базироваться только на рейтинге.

3. Формируется окончательный список риск-переменных. В примере риск-переменными будут цена сбыта и объем сбыта.

Выбор закона распределения вероятностей. Если не оговорено ус­ловие вероятностной зависимости риск-переменных, то считается, что переменные независимы и подчиняются некоторому закону распределения.

Закон распределения задает вероятность выбора значений в рамках определенного диапазона. Стандартные инвестиционные расчеты используют один вид распределения вероятностей для всех проектных переменных, включенных в расчетную модель: детерми­нированное распределение, когда конкретное единственное значе­ние переменной выбирается с вероятностью, равной единице (р = 1). Следовательно, базовая модель инвестиционного проекта может рассматриваться как детерминированный анализ и частный случай имитационной модели для детерминированных риск-переменных.

Для каждой риск-переменной, являющейся случайной величи­ной, в процессе создания модели необходимо подобрать вид рас­пределения. Подбор закона распределения сложен прежде всего из- за ограниченности статистических данных. При наличии достаточ­ного количества информации предлагается для более точного под­бора закона распределения осуществлять его методами математиче­ской статистики (проверка гипотезы о согласованности выборочных данных с подобранным законом распределения, например с помо­щью критерия х²).

При оценке законов распределения экспертным методом адек­ватность таких результатов оценить сложнее. Подход, связанный с использованием субъективных вероятностей экспертов, иногда кри­тикуют. В первую очередь это связывается с психологическими трудностями в оценке вероятностей. С другой стороны, существуют методы, с помощью которых можно избежать психологических «ло­вушек» при организации опросов и улучшить качество их результа­тов. С учетом важности дополнительной информации при приня­тии решений использование экспертов необходимо.

На практике чаще всего используют нормальный, треугольный, равномерный, дискретный законы распределения вероятностей.

Алгоритм подбора закона распределения:

1) определить возможные границы изменения риск- переменной (границы диапазона);

2) выбрать общий вид закона распределения;

3) с учетом диапазона изменения переменной и общего вида оценить основные числовые характеристики закона распределения (непрерывный случай) или приписать возможным значениям риск- переменной вероятности их реализации (дискретный случай).

1. Установление границ диапазона. Границы диапазона опреде­ляются через постулирование минимальных и максимальных значе­ний, в пределах которых могут изменяться (по предположениям проектного аналитика или эксперта) значения проектных перемен­ных. В дискретном распределении также необходимо определить поддиапазоны, которые расположены в пределах границ, обозна­ченных максимальным и минимальным значениями.

Процесс определения границ диапазона для проектных пере­менных осуществляется на основе изучения всей доступной ин­формации: статистики, мнений и оценок экспертов и т.д.

2. Подбор вида закона распределения и оценка его числовых характеристик. Подбор теоретического закона распределения, зада­ние математического ожидания и дисперсии — наиболее сложные задачи как с математической, так и с содержательной точек зрения.

Например, нормальное, треугольное и равномерное распределе­ния вероятностей симметричны, но обладают разным разбросом относительно среднего значения, таким образом, для их задания необходимо установить границы диапазона, математическое ожида­ние и дисперсию. Значения этих ключевых характеристик могут быть получены экспертным путем и на основе анализа статистики.

Наиболее часто используемый тип распределения вероятностей — дискретное. Эксперту предлагается определить интервалы и припи­сать вероятности каждому интервалу или значению.

Как следует из сказанного, процесс приписывания законов рас­пределения в значительной степени творческий, требует анализа различного вида информации и плохо поддается формализации.

В зависимости от наличия информации предлагается использо­вать один из трех подходов к подбору закона распределения и оценке его характеристик:

• обработка имеющейся статистики (по объему сбыта и др.);

• экспертное заключение;

• выбор равномерного распределения, отражающего наличие малого количества информации о переменной (только диапазоны изменения).

Точность подбора закона распределения (прежде всего точность оценки характеристик распределения) при заданных границах из­менения риск-переменных непосредственно влияет на качество мо­дели и точность оценки распределения NPV (результат модели).

Пример. В расчете инвестиционного проекта производства труб посмотрим, насколько сильно отличаются результаты имитацион­ного моделирования при выборе только треугольного распределе­ния или только равномерного распределения риск-переменных. При проведении количественного риск-анализа были установлены следующие риск-переменные (объемы продаж указаны в км труб, цены — в ден. ед. за 1 км труб):

• объем продаж в первый, во второй, в третий год; цена про­даж.

Было сделано предположение, что все риск-переменные — не­зависимые случайные величины (табл.8).

Таблица.8. Риск-переменные Название переменной Значение переменной Минимальное значение Максимальное значение Объем продаж в 1-й год       Объем продаж во 2-й год       Объем продаж в 3-й год       Цена продаж       NPV 3 545     1. Результаты для 200 испытаний при равномерном распределении риск-переменных:

математическое ожидание NPV 3487,18;

стандартное отклонение NPV 2008,76;

коэффициент вариации NPV 0,58;

минимальное значение NPV —452,48;

максимальное значение NPV 8242,59;

вероятность реализации неэффективного проекта 0,03.

Гистограмма при равномерном распределении риск-переменных показана на рис. 2.

Рис. 2. Гистограмма NPV при равномерном распределении риск-переменных

2. Результаты для 200 испытаний при треугольном распределении риск-переменных:

математическое ожидание NPV 3423,48;

стандартное отклонение NPV 1250,92;

коэффициент вариации NPV 0,37;

минимальное значение NPV 370,98;

максимальное значение NPV 6312,89;

вероятность реализации неэффективного проекта 0.

Гистограмма при треугольном распределении риск-переменных показана на рис. 3.

Рис. 3. Гистограмма NPV при треугольном распределении риск-переменных

Этот пример хорошо иллюстрирует, что уточнение вида распре­деления проекта приводит к изменению результатов. Проект с тре­угольным распределением риск-переменных (при одинаковом диа­пазоне их изменения) обладает большей устойчивостью. Во втором случае получение отрицательного NPV практически невероятно, а коэффициент вариации, характеризующий относительный разброс значений NPV, намного ниже (0,37 по сравнению с 0,58 при рав­номерной распределенности риск-переменных).

Учет вероятностной зависимости риск-переменных. Отсутствие учета вероятностной зависимости переменных, в частности коррели­рованное™, может привести к заметным искажениям результатов статистического моделирования. Включение вероятностно зависимых риск-переменных в математическую модель инвестационного проек­та может привести к серьезным искажениям характеристик устойчи­вое™ и устойчивости проекта, если условие зависимое™ не будет учтено в математической модели. Степень смещения результатов за­висит от важное™ вероятаостно зависимых переменных по отноше­нию к проекту. Поэтому проводится специальный этап установления наличия вероятностной зависимости, в частности корреляции между переменными и поиска возможностей ее учета в модели. Это касает­ся как парной, так и множественной корреляции.

Пример. Рассмотрим результаты моделирования на том же при­мере, на котором изучали влияние вида закона распределения риск- переменных на результаты моделирования. Анализ будем проводить для случая равномерной распределенности случайных величин. Пусть после проведения дополнительных исследований было уста­новлено наличие линейной корреляции между объемом продаж и ценой.

Допустим, что по исходным данным известно, что коэффициент регрессии в уравнении связи между ценой и объемом сбыта равен —0,7 (что показывает отрицательную сильную линейную зависи­мость между объемом продаж и ценой на продукцию, что, по сути, отражает закон спроса). Тогда, уравнения регрессии, учитываемые в модели, выглядят так:

Объем продаж в 1-й год = 310 — 0,7 • Цена продаж;

Объем продаж во 2-й год = 399 — 0,7 • Цена продаж;

Объем продаж в 3-й год = 399 — 0,7 • Цена продаж.

Рассмотрим результаты расчетов, проведенных по данной моде­

ли (рис.4):

математическое ожидание NPV 3492,90;

стандартное отклонение NPV 123,39;

коэффициент вариации NPV 0,04;

минимальное значение NPV 3075,40;

максимальное значение NPV 3760,86;

вероятность реализации неэффективного проекта 0.

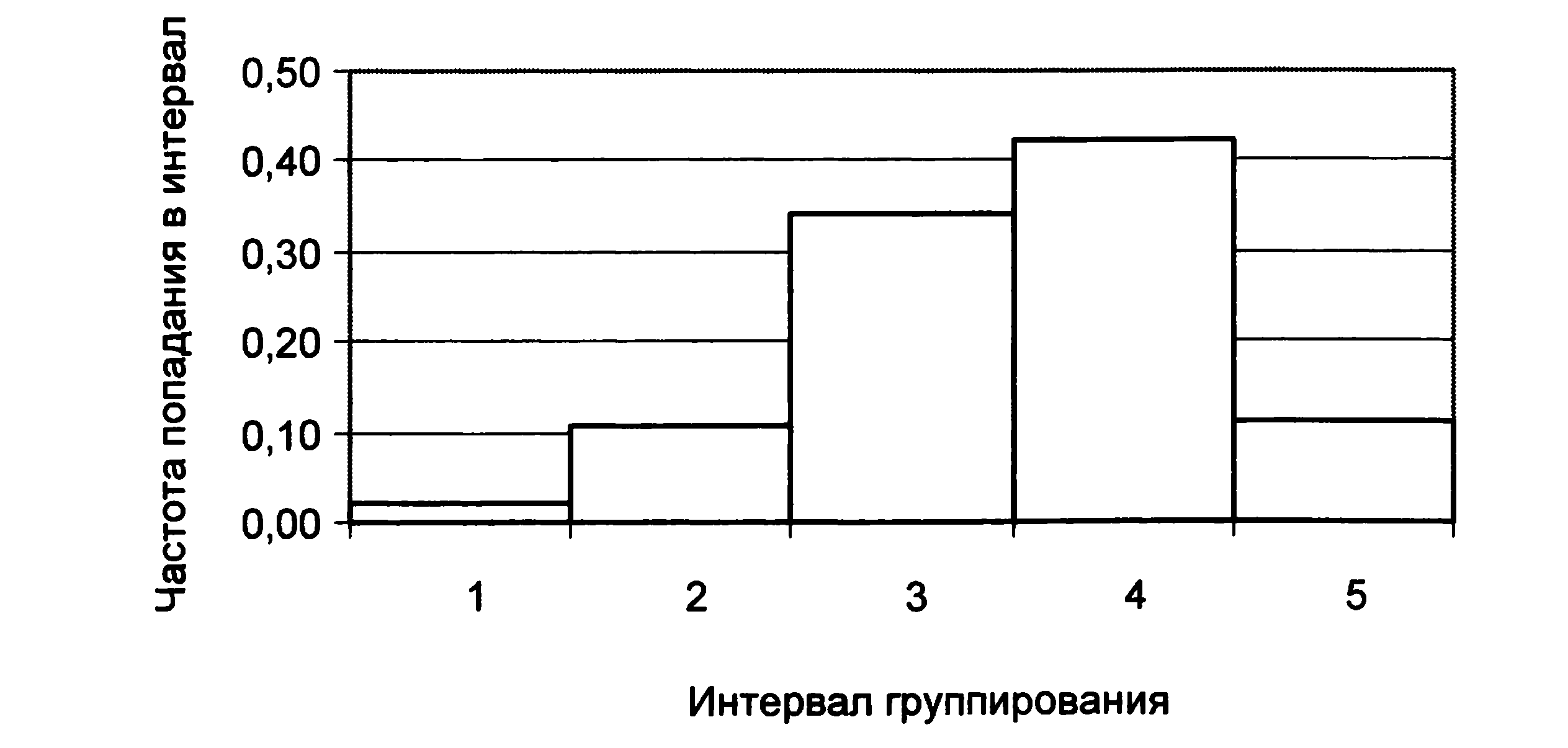
Рис. 4. Гистограмма NPV при учете вероятностной зависимости риск-переменных

Очевидно, что полученные результаты существенно отличаются от модели, в которой все эти риск-переменные считались незави­симыми. Учет корреляции уточняет модель. Проект, как выясняет­ся, обладает значительным запасом прочности и очень надежный. Коэффициент вариации снизился с 0,58 до 0,04, а вероятность реа­лизации неэффективного проекта — с 0,03 до 0.

Для учета зависимости между переменными могут быть исполь­зованы такие статистические методы, как, например, классическая модель линейной регрессии для моделирования корреляции; зада­ние условной функции распределения; моделирование многомерно­го нормального закона с помощью матрицы ковариаций.

2. Осуществление имитации. Основным этапом имитационного моделирования, в рамках которого с помощью компьютерной про­граммы реализован алгоритм метода Монте-Карло, является осуще­ствление имитации.

1. Генерирование случайных чисел проводится путем компью­терной операции получения псевдослучайных чисел, независимых и равномерно распределенных на отрезке [0; 1]. Каждое новое полу­ченное случайное число рассматривается как значение функции распределения для соответствующей риск-переменной.

2. Значение каждой независимой риск-переменной восстанав­ливается как аргумент функции распределения вероятности данной риск-переменной. При этом учитываются условия наличия вероят­ностной зависимости и коррелированное™.

3. Значения переменных величин подставляются в математиче­скую модель, и рассчитывается интегральный показатель эффек­тивности проекта (например, NPV).

4. Изложенный в пп. 1—3 алгоритм повторяется п раз. Результа­ты моделирования (т.е. NPV проекта или другой показатель), таким образом, рассчитываются и сохраняются для каждого имитационно­го эксперимента.

Каждый имитационный эксперимент — это случайный сценарий. Число имитационных экспериментов должно быть достаточно вели­ко, чтобы сделать выборку репрезентатавной по отношению к бес­конечному числу возможных комбинаций. Ни в коем случае нельзя выбирать п произвольно. Необходимое число имитационных экспе­риментов зависит от многих факторов, например от структуры мате- матаческой модели, степени детализации модели денежных потоков, числа и диапазонов изменения риск-переменных. В одном случае будет достаточным п = 100, а в другом — необходимо провести более 5000 расчетов. Поэтому следует осуществлять столько эксперимен­тов, сколько требуется, чтобы обеспечить необходимую точность мо­делирования и надлежащее качество результатов имитации.

Некоторые подходы к правильному выбору количества реализаций при имитационном моделировании рассмотрены в приложении 1.

2. Анализ результатов. На последнем этапе процесса риск- анализа проводится анализ и интерпретация результатов, получен­ных на этапе имитации.

Можно проводить анализ результатов имитационного модели­рования двух типов: графический и количественных показателей.

Результатом проведения имитационных экспериментов является выборка из п значений NPV (или другого результирующего показа­теля). Вероятность каждого случайного сценария равна

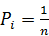(6.2)

Где i — номер сценария;

п — общее число имитационных экспериментов.

Следовательно, вероятность того, что проектный результат будет ниже определенного значения, — это просто число расчетов, при которых значение показателя было ниже, поделенное на общее число имитационных экспериментов. Строя график кумулятивного распределения частот появления результатов, можно рассчитать ве­роятность, соответствующую результатам проекта, которые будут ниже или выше заданного значения.

Графический анализ. Для проведения графического анализа не­обходимо построить выборочные аналоги функции распределения и функции плотности распределения результирующего показателя (NPV или другого). В проектном анализе они называются соответ­ственно куммулятивным профилем риска и профилем риска.

Таким образом, необходимо построить гистограмму NPV. По полученной выборке из NPV строится вариационный ряд, т.е. зна­чения NPV ранжируются от минимального до максимального. Гис­тограмма строится путем разбиения вариационного ряда на к ин­тервалов группирования в соответствии с рекомендациями матема­тической статистики (к = Ln(п), например).

При необходимости можно подобрать и теоретический закон распределения результирующего показателя; для этого оценивается согласованность эмпирических данных с подбираемым законом распределения с помощью критерия согласия x²..

Стандартные критерии принятия инвестиционного решения, обычно применяемые в детерминированном анализе, сохраняют свое значение ценность и сопоставимость и для данного метода.

Однако имитационное моделирование предоставляет лицу, при­нимающему решение, дополнительную информацию о рискованно­сти проекта (какие случайные сценарии с какой вероятностью мо­гут реализоваться), поэтому окончательное решение субъективно.

Общее правило состоит в том, что выбирается проект с распреде­лением вероятностей NPV, которое больше соответствует личной предрасположенности к риску лица, принимающего решение. Если ЛПР склонно к риску, оно скорее будет выбирать для инвестирова­ния проекты с относительно высоким средним значением NPV, об­ращая меньше внимания на их возможную рискованность (большой разброс относительно среднего значения, значительную вероятность реализации неэффективного проекта и т.д.). Если ЛПР не располо­женно к риску, оно, скорее всего, выберет для инвестирования про­екты с не очень большим средним NPV, но малорискованные.

Для иллюстрации возможностей графического анализа (подоб­ранных теоретических законов распределения) рассмотрим некото­рые возможные ситуации, связанные с принятием решения по един­ственному проекту (случаи 1—3) и связанные с выбором одного из альтернативных (взаимоисключающих) проектов (случаи 4 и 5).

Кумулятивное распределение вероятностей NPV более часто применяется для принятия решений, касающихся взаимоисклю­чающих проектов, в то время как некумулятивное (плотность) луч­ше применять для выявления моды и среднего значения.

Случай 1. Случайная величина NPV является положитель­ной (рис. 6.5). Если значение NPV положительно даже в «наихуд­шем» случае, проект может быть принят.

Плотность распределения вероятностей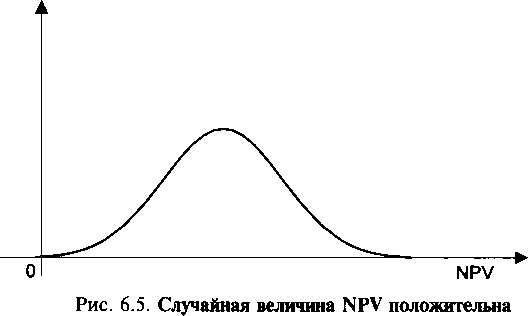

Случай 2. Случайная величина NPV отрицательна (рис. 6.6). Если даже в «наилучшем» случае получается отрицательное значе­ние NPV (т.е. вероятность реализации эффективного проекта равна нулю), проект должен быть отвергнут.

Плотность распределения 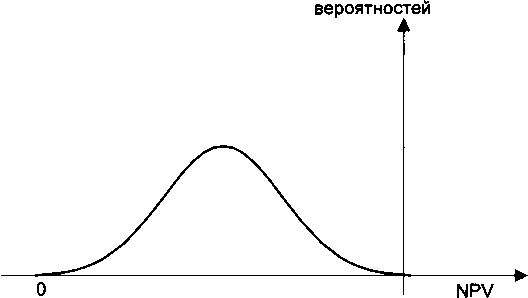Рис. 6.6. Случайная величина NPV отрицательна

Случай 3. Случайная величина NPV может быть любой (рис. 6.7). Существует некоторая вероятность того, что NPV прини­мает положительные значения, и некоторая вероятность того, что NPV будет отрицательна, поэтому судьба проекта зависит от пред­расположенности к риску лица, принимающего решение.

Плотность распределения вероятностей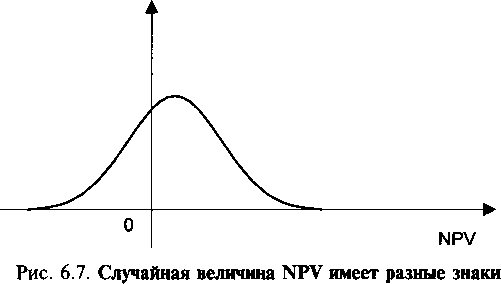

Случай 4. Непересекающиеся графики кумулятивных рас­пределений вероятностей NPV для взаимоисключающих проектов (рис. 6.8). При одинаковой вероятности NPV проекта 2 всегда больше, чем проекта 1. Поэтому, если графики кумулятивных рас­пределений вероятностей NPV для взаимоисключающих проектов не пересекаются ни в одной точке, то следует выбирать проект, график функции распределения вероятностей которого лежит пра­вее. При небольшом сдвиге функций распределения нельзя исклю­чить предположения, что он вызван только разбросом статистиче­ских данных, а не объективным преимуществом одного проекта перед другим. Данный случай может быть исследован особо, путем проверки гипотезы о расположении функций распределения (на­пример, с помощью критерия Вилкоксона).

Вероятность 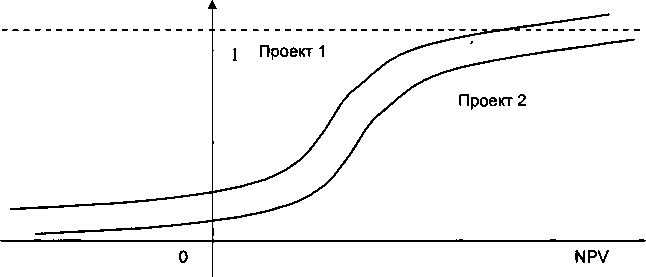Рис. 6.8. Непересекающиеся графики функций распределения вероятностей NPV для взаимоисключающих проектов

Случай 5. Пересекающиеся кумулятивные распределения плотности вероятностей NPV для взаимоисключающих проектов (рис. 6.9—6.11). Склонных к риску ЛРП будет привлекать возмож­ность высокого NPV, и поэтому они выберут проект 1. Несклонные к риску будут ориентироваться на меньшие потери, поэтому они вы­берут проект 2. Если распределения вероятностей NPV для взаимо­исключающих проектов пересекаются в какой-либо точке, решение остается зависимым от предрасположенности к риску и расположе­ния точки пересечения. С некумулятивным распределением вероят­ностей реальные пересечения труднее определить, так как вероят­ность представлена визуально как общая площадь под такой кривой.

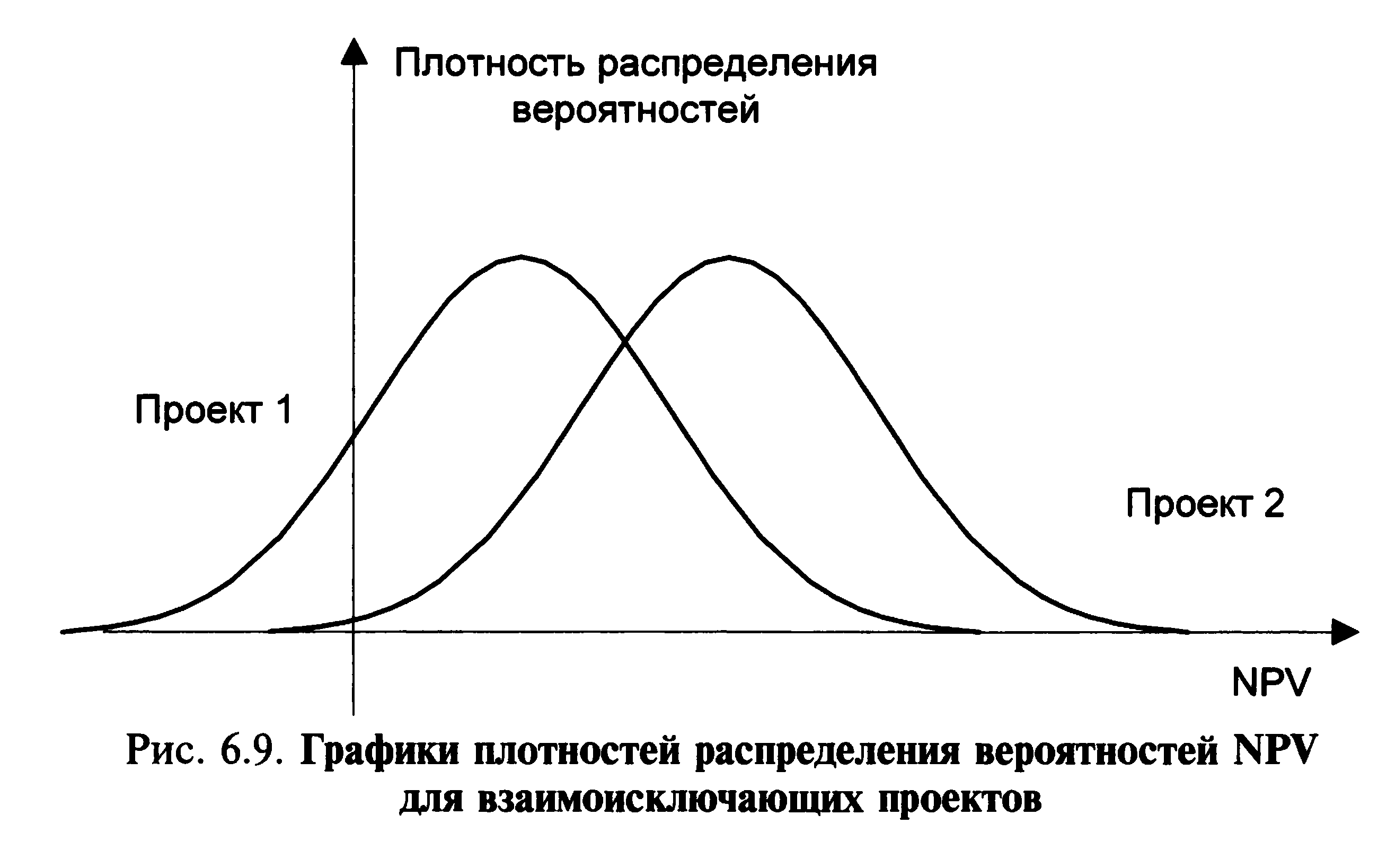
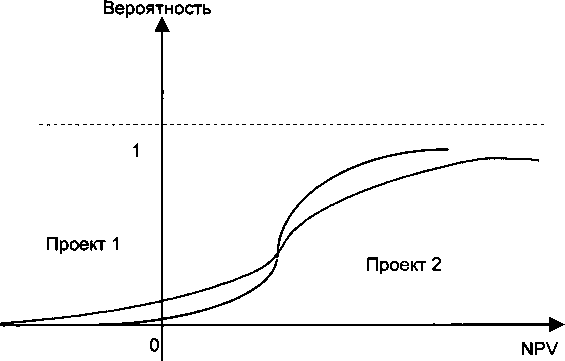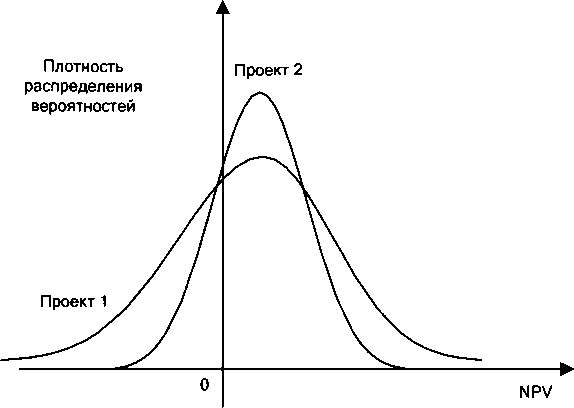Рис. 6.10. Пересекающиеся графики функций распределения вероятностей NPV для взаимоисключающих проектов

Рис. 6.11. Пересекающиеся графики плотностей распределения вероятностей NPV для взаимоисключающих проектов

В данной ситуации для формализации результатов визуального анализа можно проверить гипотезу о сравнении дисперсий с помо­щью критерия Фишера или критерия Романовского. Если гипотеза о равенстве дисперсий отвергается, то проект с меньшей дисперси­ей более надежен. Другое основание для принятия решений может дать сравнение вероятностей получения NPV ниже заданного поро­гового уровня.

Анализ количественных показателей. Ниже описываются количе­ственные измерители риска для NPV, но аналогичные расчеты мо­гут быть проведены и для других показателей эффективности инве­стиционного проекта.

Ожидаемое значение. Показатель «ожидаемое значение» EV (expected value) представляет собой агрегирование в виде единст­венного числа информации, имеющейся в распределении вероятно­стей NPV. Он рассчитывается как взвешенная средняя значений всех возможных результатов (как было отмечено выше, все случай­ные сценарии равновероятны, поэтому 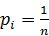где п — общее число проведенных имитационных экспериментов):

Ожидаемое значение NPV при анализе проекта в ситуации не­определенности позволяет, заменив стандартный критерий одного значения NPV, провести оценку эффективности проекта и сравнить эффективность альтернативных проектов, так как учитывает риск (множество возможных значений NPV при случайных сценариях) и соответствует аксиомам рационального поведения. С другой сторо­ны, этот показатель не дает полной информации о степени риско­ванности проекта в целом самого по себе и по сравнению с други­ми проектами, для выполнения такого анализа целесообразно ис­пользовать иные критерии, речь о которых пойдет ниже.

Может применяться как для оценки коммерческой эффектив­ности проекта в целом, так и для оценки эффективности проекта с учетом схемы финансирования.

Ожидаемый выигрыш. Показатель «ожидаемый выигрыш» EG (expected gains) определяется как сумма «взвешенных по вероятно­стям» положительных значений NPV:

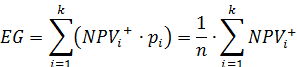
где 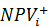— число неотрицательных значений NPV;

к — число неотрицательных значений NPV в полученной в результате проведения имитационных экспериментов вы­борке случайных сценариев.

Может применяться для оценки коммерческой эффективности проекта в целом. Для оценки проекта с учетом схемы финансиро­вания совпадает с показателем ожидаемого дохода при выполнении условия финансовой реализуемости проекта.

Ожидаемые потери. Показатель «ожидаемые потери» EL (expected losses) определяется как сумма «взвешенных по вероятно­стям» отрицательных значений NPV:

где 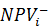— отрицательные значения NPV;

т — число отрицательных значений NPV в полученной в ре­зультате проведения имитационных экспериментов вы­борке случайных сценариев.

Может применяться как для оценки коммерческой эффектив­ности проекта. Для оценки проекта с учетом схемы финансирова­ния не применяется, так как величина ЧДД в этом случае в сцена­риях при выполнении условия финансовой реализуемости положи­тельна.

Ожидаемое значение есть сумма ожидаемого выигрыша и ожи­даемых потерь:

EV =EG + EL.

Коэффициент ожидаемых потерь. Этот показатель аналогичен показателю «нормируемый ожидаемый убыток». Коэффициент ожидаемых потерь ELR (expected loss ration) является показателем, измеряющим величину взятых по модулю ожидаемых потерь по отношению к сумме ожидаемого выигрыша и взятых по модулю ожидаемых потерь:

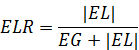
Коэффициент ожидаемых потерь, определенный таким образом, может изменяться от 0, означающего отсутствие ожидаемых потерь и низкую рискованность проекта, до 1, которая означает отсутствие ожидаемого выигрыша и полную рискованность проекта.

Этот показатель можно считать хорошим измерителем риско­ванности при расчетах коммерческой эффективности проекта, так как он является безразмерной величиной и измеряет риск как воз­можность потерь. При этом он учитывает не только возможность возникновения неэффективных проектов, но и размеры возможных потерь и доходов.

Дисперсия и среднее квадратическое отклонение. Дисперсия D и среднее квадратическое отклонение S показывают, насколько велик разброс значений NPV относительно ожидаемого значения. Это абсолютные измерители риска. Показатели применимы в первую очередь для оценки риска портфельных инвестиций, так как рас­сматривают риск как возможность и отрицательных, и положитель­ных отклонений от среднего значения (и потерь, и выигрыша). Именно из-за этого они мало пригодны для целей оценки риска проекта как возможности потерь.

Дисперсия рассчитывается по формуле

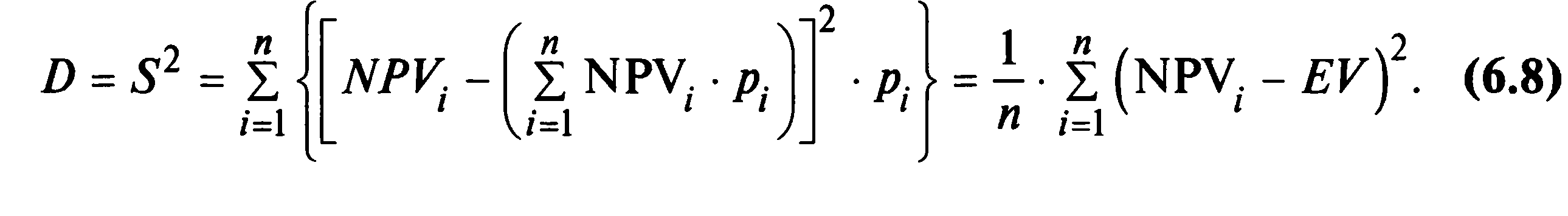
Среднее квадратическое отклонение определяется как корень из дисперсии:

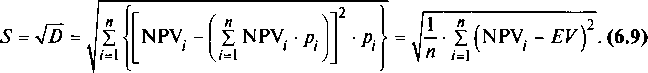Коэффициент вариации Var является относительным показателем риска, так как абсолютное значение риска (среднего квадратическо­го отклонения) нормируется на значение ожидаемого дохода. Он рассчитывается по формуле

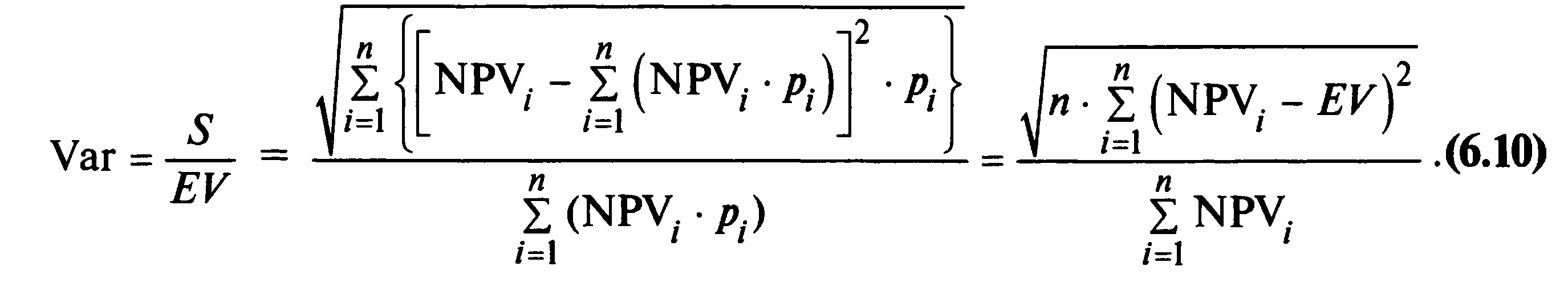
При положительном математическом ожидании чем ниже ко­эффициент вариации, тем меньше разброс показателя эффективно­сти ИП относительно его ожидаемого значения. Недостатком ко­эффициента вариации для целей анализа риска инвестиционных проектов является то, что он, как и предыдущие индикаторы, учи­тывает и отрицательные, и положительные отклонения от ожидае­мого значения.

Вероятность реализации неэффективного проекта Р является, по сути, относительной частотой появления неэффективного проекта, относительным (безразмерным) показателем и позволяет определять риск как возможность осуществления неэффективного проекта. Может рассматриваться как показатель рискованности проекта при расчетах коммерческой эффективности проекта в целом без учета источников финансирования. К числу его недостатков можно отне­сти тот факт, что он показывает, сколько раз было нарушено усло­вие эффективности, но не показывает, насколько велики потери. Вероятность реализации неэффективного проекта рассчитывается по формуле

P(NPV 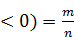(6.11)

где т — число отрицательных значений NPV в полученной выборке; п — число проведенных имитационных экспериментов (размер вы­борки).

Вероятность реализации проекта со значением критериального показателя ниже порогового уровня. Вероятность реализации проекта Р* со значением критериального показателя ниже порогового уров­ня показывает относительную частоту появления такого проекта, служит относительным измерителем риска прежде всего с позиции отдельных участников проекта, которые сами выбирают интере­сующий их критерий (Criter) и устанавливают минимально прием­лемое для них его значение (Criter*).

Р* (Criter < Criter*) = , (6.12)

где т — число ИЭ со значением критериального показателя (Criter) ниже порогового уровня (Criter*), задаваемого лицом, оцени­вающим риск,

п — общее число экспериментов (значений показателя Criter в вы­борке).

Этот индикатор трактует риск как возможность потерь и может использоваться как показатель рискованности при расчетах эффек­тивности участия в проекте. Его недостаток заключается в том, что, показывая, сколько раз было нарушено условие эффективности, он не показывает, насколько велики потери.

Таким образом, на основе имеющейся характеристики измери­телей риска инвестиционного проекта можно сделать вывод, что наилучший показатель оценки эффективности проекта по результа­там имитационного моделирования методом Монте-Карло — это ожидаемое значение NPV, а для оценки рискованности проекта лучше использовать вероятность реализации неэффективного про­екта и коэффициент ожидаемых потерь (оба этих индикатора риска обладают свойством безразмерное™, что позволяет с их помощью сравнивать рискованность альтернативных проектов, обеспечивает сопоставимость сравнения уровня риска для различных проектов).

Вероятностная имитационная модель оценки рисков. Преимущества использования имитационного моделирования методом Монте-Карло в российской экономике обусловлены следующими причинами:

• высокая неопределенность приводит к тому, что результаты реализации проекта существенно отличаются от прогнозных, по­этому для избежания серьезных потерь необходимо оценить, какова вероятность реализации неэффективного проекта;

• различного рода высокие риски, присутствующие в россий­ской экономике, требуют от разработчиков проекта реализации ме­роприятий по управлению рисками, с помощью предлагаемого под­хода можно заранее оценить, насколько те или иные мероприятия по управлению рисками смогут снизить рискованность проекта и как это отразится на эффективности проекта.

Итак, имитационное моделирование методом Монте-Карло мо­жет быть использовано:

• для оценки рисков инвестиционного проекта;

• для управления рисками инвестиционного проекта;

• для построения оптимизационных моделей управления рис­ками с целью выбора минимального уровня риска при заданной ожидаемой чистой дисконтированной стоимости проекта или мак­симальной эффективности проекта при заданном пороговом уровне риска.

^[1] В дальнейшем также речь будет идти об NPV как о наиболее часто употреб­ляемом и наиболее универсальном показателе интегральной эффективности проекта, хотя в принципе все последующие рассуждения можно применять и к другим показателям эффективности.

^[2] Metropolis N., Ulam S. The Monte Carlo Method// J. Amer. Statistical Assoc. 1949. V. 44. № 247.

^[3] А.Г. Быковой, автором п. 6.4, была разработана обучающая программа в EXCEL, позволяющая выполнять основные этапы имитационного моделирования.