Занятие 6 Тема: Построение и базовый анализ классической линейной модели множественной регрессии
Методические указания
Модель множественной линейной регрессии можно представить в виде:
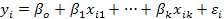 (1)
(1)
где i = 1, 2, …, n число наблюдений.
εi – регрессионные ошибки случайного характера,
yi – i-е наблюдение зависимой переменной,
xi1, xi2,… xik. – i-е наблюдение объясняющих переменных,
β0,β1 …βk – неизвестные параметры модели.
Пусть:
Y обозначает 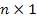 матрицу (вектор-столбец) (y1,…, yn)Т (Т вверху означает транспонирование),
матрицу (вектор-столбец) (y1,…, yn)Т (Т вверху означает транспонирование),
β = (β0, β1, …, βк)Т – 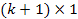 вектор-столбец коэффициентов (неизвестных значений параметров модели),
вектор-столбец коэффициентов (неизвестных значений параметров модели),
ε = (ε1, ε2, …, εn)Т – 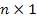 вектор-столбец ошибок,
вектор-столбец ошибок,
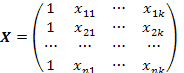 -
- 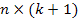 матрицу объясняющих переменных, которая соответствует набору векторов-столбцов объясняющих переменных, а также вектору-столбцу из единиц, отвечающему за константу в уравнении модели. Матрица должна быть матрицей полного ранга.
матрицу объясняющих переменных, которая соответствует набору векторов-столбцов объясняющих переменных, а также вектору-столбцу из единиц, отвечающему за константу в уравнении модели. Матрица должна быть матрицей полного ранга.
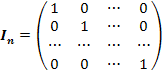 - единичная матрица размерности
- единичная матрица размерности 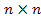 ;
;
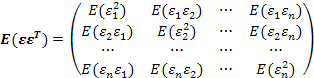 - ковариационная матрица размерности
- ковариационная матрица размерности 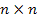 вектора ошибки.
вектора ошибки.
Гипотезы, лежащие в основе множественной регрессии в матричной форме выглядят следующим образом:
1. Y=Xβ+ε – спецификация модели;
2. X – детерминированная матрица, имеет максимальный ранг k+1;
3. a,b. E(ε)= 0; V(ε)=E(εεT)=σ2 In;
дополнительное условие:
3. с. ε ~N(0,σ2 In ), т.е. ε – нормально распределенный случайный вектор со средним 0 и матрицей ковариаций σ2 In (нормальная линейная регрессионная модель).
Оценкой этой модели по выборке является уравнение:
Y = X 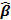 + e,
+ e,
Где 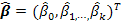 – вектор-столбец оценок неизвестных параметров модели;
– вектор-столбец оценок неизвестных параметров модели;
e = (e1, e2, …, en)Т – вектор –столбец регрессионных остатков.
Оценка неизвестных параметров модели методом наименьших квадратов:
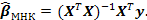 (2)
(2)
Пусть 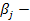 истинное значение j-го коэффициента регрессии. Тогда статистика
истинное значение j-го коэффициента регрессии. Тогда статистика
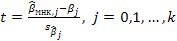 (3)
(3)
распределена по закону Стьюдента (t-распределения) с n-k-1 степенями свободы.
Из (3) получаем, что интервал
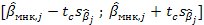
является 100(1-α)%-ным доверительным интервалом для истинного значения коэффициента 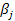 , где
, где 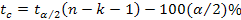 -ная точка распределения Стьюдента с n-k-1 степенями свободы.
-ная точка распределения Стьюдента с n-k-1 степенями свободы.
При проверке гипотезы Ho: βj=0 t-статистика выглядит 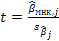
Значение 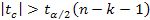 позволяет сделать вывод об отличии от нуля (на уровне значимости α) заданного коэффициента регрессии и, следовательно, о наличии влияния (связи) Xj на Y.
позволяет сделать вывод об отличии от нуля (на уровне значимости α) заданного коэффициента регрессии и, следовательно, о наличии влияния (связи) Xj на Y.
Общей характеристикой модели может служить коэффициент детерминации R2 и F-статистика модели:
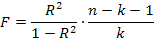
В предположении справедливости гипотезы о том, что все коэффициенты модели, кроме константы, равны нулю, т.е. β1= β2= … =βк=0 в условиях нормальной линейной модели множественной регрессии, F-статистика должна подчиняться распределению Фишера со степенями свободы (k, n-k-1). Следовательно справедливость этой гипотезы можно проверить следующим образом. По заданному критерию значимости α из таблиц определяют 100α%-ую точку F(k, n-k-1)-распределения fα(k, n-k-1). Если окажется, что
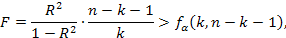
то гипотеза об отсутствии линейной связи между переменной Y и объясняющими переменными отвергается (с вероятностью ошибки, равной α), и принимается – в противном случае.
Задание 1. Построить для следующих данных из таблицы 1 линейную модель множественной регрессии и провести её базовый анализ в предположении, что построенная модель является нормальной моделью множественной регрессии.
Таблица 1. Исходные данные для модели множественной регрессии
| N п/п | Y | X1 | X2 |
Построение модели:
1. Матрица объясняющих переменных, вектор зависимой переменной:
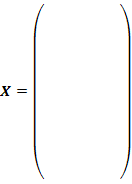
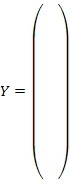
2. Вычисление коэффициентов модели 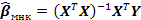 :
:

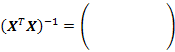

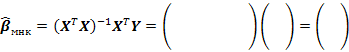
3. Регрессионное уравнение модели:
Базовый анализ нормальной линейной модели множественной регрессии:
1. Несмещенная оценка дисперсии ошибок σ2:
s2= 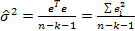
Вектор остатков регрессии:


s2= 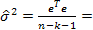
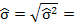
 2015-05-18
2015-05-18 273
273







