Для того чтобы найти волновую функцию y, характеризующую состояние микрочастицы или системы микрочастиц, необходимо решить волновое уравнение, которое было получено Э. Шредингером в 1926 г. Уравнение Шредингера — основа квантовой (волновой) механики, так же как уравнения Ньютона — основные уравнения классической механики. Как и уравнения Ньютона, уравнение Шредингера не может быть выведено из других более элементарных принципов и вводится в квантовую механику как постулат. Справедливость уравнения Шредингера определяется тем, что все выводы, полученные из его решений и доступные опытной проверке, подтверждались. Тем не менее, дадим некоторое методическое обоснование этого уравнения.
Продифференцируем дважды по координате x волновую функцию (8):
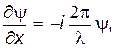
| |
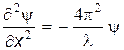
|
или
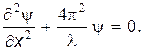
| (12) |
Подставим вместо длины волныl ее значение по формуле де Бройля:
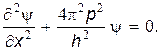
|
Учитывая, что
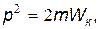
|
где Wк — кинетическая энергия частицы, получаем
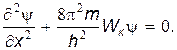
|
Заменив в этом уравнении кинетическую энергию частицы на разность между полной и потенциальной энергией: Wк =W–Wр. Тогда
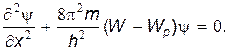
| (13) |
Последнее уравнение и представляет собой одномерное стационарное уравнение Шредингера. Если ввести постоянную ħħ=h/2p, то уравнение (13) можно переписать в виде
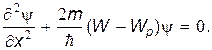
| (14) |
В общем (трехмерном) случае уравнение Шредингера имеет вид
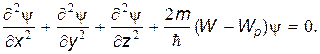
| (15) |
В тех случаях, когда потенциальная энергия системы изменяется со временем, необходимо использовать более сложное временное уравнение Шредингера:
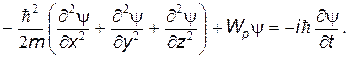
|
 2015-05-18
2015-05-18 490
490








