Таким методом является обобщенный мнк. Он учитывает переменную дисперсию.
Обозначается ОМНК(GLS) для объяснения процессов происходящих в текущем периоде.Причем лаговыми переменными могут быть как зависимые переменные, так и независимые.
Одним из методов устранения автокорреляции остатков является процедура Оркатта-Кокроуна.
Рассмотрим уравнение регрессиии
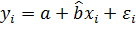 , (4.1)
, (4.1)
где 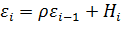 , (4.2)
, (4.2)
где Hi – случайная компонента
Запишим уравнение (4.1) для предложеного периода i-1 и умножим все уравнения на 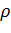 :
:
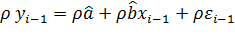
Вычтим из (4.1)
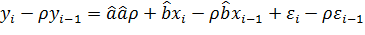
По (4.2):
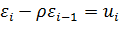
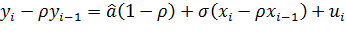
Пусть 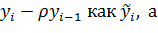
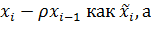
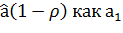
Тогда 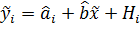 (4.3)
(4.3)
Если известно 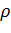 , то можно найти
, то можно найти 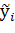 и
и 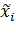 через уi, yi-1, xi, xi-1.
через уi, yi-1, xi, xi-1.
А затем рассчитать регрессию между 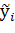 и
и 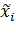
Процедура Оркатто-Кокроуна
1.Оценивается уравнение (4.1) находятся коэффециенты 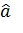 и
и 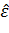 .И находят остатки
.И находят остатки 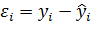
ОМНК принимается не только для оценки данных для которых существенна гетероскедостичность остатков, но и для данных, для которых имеется место автокорреляции остатков т.е оценки, оцененные ОМНК, будут обладать как свойством несмещенности, так и иметь наименьшее выборочное диспресии.
Предположим, что матожидание равно 0, а диспресия, которая изменяется, пропорционально величине хi
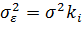 (4.5), где
(4.5), где
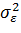 –дисперсия ошибки при конкретном суммарном значении ф-ра.
–дисперсия ошибки при конкретном суммарном значении ф-ра.
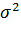 – постоянная дисперсия ошибки при соблюдении условия гомоскедастичности остатков.
– постоянная дисперсия ошибки при соблюдении условия гомоскедастичности остатков.
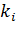 – коэффициент пропорциональности, изменяющийся с изменением ф-ра.
– коэффициент пропорциональности, изменяющийся с изменением ф-ра.
Тогда уравнение регрессии с дисперсии имеющий вид (4.5), можно преобразовывать в новое уравнение:
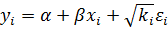
т.к Д=М((х-М(х))2 и Д=М(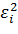 )
)
Для другого уравнения гетероскедостичность по-прежнему существует. Разделим данное уравнение на 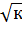
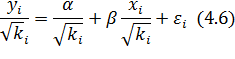
Тогда дисперсия для полученного уравнения будет постоянной и равна
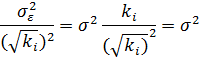
Обозначим 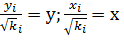
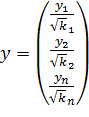 ;
; 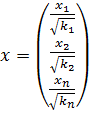 (4.7)
(4.7)
Определение 4.1. Уравнение регрессии (4.6) с переменными вида (4.7) называется взвешенным уравнением регрессии, где весами являются выражение 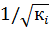 .
.
Оценка коэффициентов для точки 0 определенной регрессии осуществляется на основании взвешенной МНК (ВМНК), в которой следует минимизировать функционал 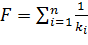 (y-a-b xi)2
(y-a-b xi)2 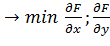 приравниваем к 0
приравниваем к 0
Получаем систему нормальных уравнений для оценки а и b
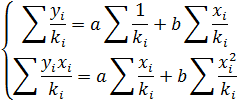
Откуда следует
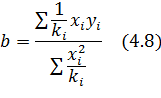
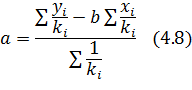
Как видно параметры регрессии определенные по формуле (4.8), полностью зависит от гипотезы выдвигаемой относительно коэффициентов пропорциональности К; обычно предполагается, что остатки 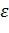 I т.е имеем параметры
I т.е имеем параметры 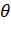 для каждого уi
для каждого уi
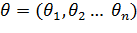
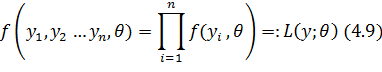
Функция 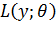 , определяется по формуле (4.9) называется функцией максимального правдоподобия.
, определяется по формуле (4.9) называется функцией максимального правдоподобия.
Иногда переходят к логарифмированной функции правдоподобия
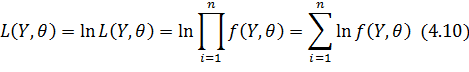
Решение по ММП предполагает нахождение таких параметров 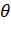 , при которых функция правдоподобия достигает максимума, т.е находит
, при которых функция правдоподобия достигает максимума, т.е находит 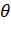 оптимальное .Нахождение
оптимальное .Нахождение 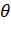 оптимальное в простых случаях производится с помощью методов матанализа (т.е приравнивающие к 0 первых производных:
оптимальное в простых случаях производится с помощью методов матанализа (т.е приравнивающие к 0 первых производных:
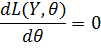
В сложных случаях используется методы оптимального программирования (симплекс метод) или с помощью методов численного анализа, основных на интерактивных процедурах.
Для нахождения параметров линейной регрессии 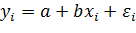 надо знать законы распределения либо зависимой переменной
надо знать законы распределения либо зависимой переменной 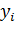 , либо остатков
, либо остатков 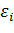 . Когда этот закон нормальный, из ММП пропорциональна значениям какого-то независимого ф-ла
. Когда этот закон нормальный, из ММП пропорциональна значениям какого-то независимого ф-ла 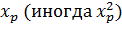
 2015-05-18
2015-05-18 290
290








