Построим таблицу значений факторных переменных Х2 = ln A, Х3 = ln k и результативной переменной Y= ln q.
| T | X2 | Х3 | У | Х 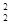
| Х 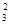
| У 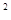
| Х 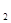 Х Х 
|
| 0,1798 | 1,1939 | -0,1278 | 0,032 328 | 1,425 397 | 0,016 333 | 0,214 663 | |
| 0,2038 | 1,2030 | -0,1009 | 0,041 534 | 1,447 209 | 0,010 181 | 0,245 171 | |
| 0,1807 | 1,1878 | -0,1290 | 0,032 652 | 1,410 869 | 0,016 641 | 0,214 635 | |
| 0,1914 | 1,1314 | -0,1404 | 0,036 634 | 1,280 066 | 0,019 712 | 0,216 550 | |
| 0,2608 | 1,0986 | -0,0823 | 0,068 017 | 1,206 922 | 0,006 773 | 0,286 515 | |
| 0,2994 | 1,0543 | -0,0587 | 0,089 640 | 1,111 548 | 0,003 446 | 0,315 657 | |
| 0,3570 | 1,0006 | -0,0182 | 0,127 449 | 1,001 200 | 0,000 331 | 0,357 214 | |
| 0,3471 | 0,9969 | -0,0294 | 0,120 478 | 0,993 810 | 0,000 864 | 0,346 024 | |
| 0,3681 | 1,0225 | 0,0000 | 0,135 498 | 1,045 506 | 0,000 000 | 0,376 382 | |
| 0,4148 | 0,9783 | 0,0334 | 0,172 059 | 0,957 071 | 0,001 116 | 0,405 799 | |
| ВСЕГО | 2,8029 | 10,8673 | -0,6533 | 0,856 289 | 11,879 598 | 0,075 397 | 2,978 610 |
| СРЕДНЯЯ | 0,28029 | 1,08673 | -0,06533 | 0,085 628 9 | 1,187 959 8 | 0,007 539 7 | 0,297 861 |
| t |
Х  У У
|
Х  У У
| У= 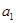 +
+ +
+ 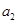 Х Х 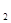 +
+ +
+ 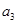 Х Х 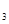
| e=У-У | e2 |
(У- 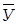 )2 )2
|
| -0,022 978 | -0,152 580 | -0,128 74 | 0,000 94 | 0,000 000 88 | 0,004 021 | |
| -0,020 563 | -0,121 383 | -0,100 59 | 0,000 31 | 0,000 000 10 | 0,001 243 | |
| -0,023 310 | -0,153 226 | -0,130 09 | 0,001 09 | 0,000 001 19 | 0,004 194 | |
| -0,026 873 | -0,158 849 | -0,140 20 | 0,000 20 | 0,000 000 04 | 0,005 606 | |
| -0,021 464 | -0,090 415 | -0,080 97 | 0,001 33 | 0,000 001 77 | 0,000 245 | |
| -0,017 575 | -0,061 887 | -0,057 79 | 0,000 91 | 0,000 000 83 | 0,000 057 | |
| -0,006 497 | -0,018 211 | -0,018 56 | 0,000 36 | 0,000 000 13 | 0,002 187 | |
| -0,010 205 | -0,029 309 | -0,030 14 | 0,000 74 | 0,000 000 55 | 0,001 238 | |
| 0,000 000 | 0,000 000 | 0,001 09 | 0,001 09 | 0,000 001 19 | 0,004 412 | |
| 0,013 854 | 0,032 675 | 0,032 65 | 0,000 75 | 0,000 00056 | 0,009 600 | |
| ВСЕГО | -0,135 611 | -0,753 185 | 0,000 00724 | 0,032 803 | ||
| СРЕДНЯЯ | -0,013 5611 | -0,075 318 5 | 0,000 000 724 | 0,003 280 3 |
1. Найдем коэффициенты уравнения линии регрессии
Y= 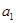 +
+ 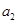 Х
Х 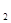 +
+ 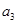 Х
Х 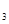
Как решение системы уравнений
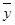 =
= 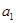 +
+ 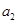
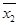 +
+ 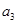
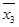

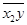 =
= 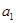
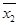 +
+ 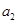
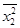 +
+ 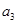
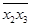
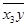 =
= 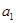
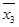 +
+ 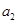
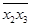 +
+ 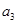
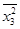
-0,065 33 = 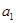 + 0,280 29
+ 0,280 29 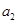 + 1,086 73
+ 1,086 73 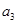
-0,013 56 = 0,280 29 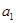 + 0,085 63
+ 0,085 63 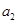 + 0,297 86
+ 0,297 86 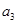
-0,075 32 = 1,086 73 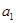 + 0,297 86
+ 0,297 86 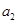 + 1,187 96
+ 1,187 96 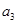
Решая систему методом Гаусса получим (решение следует привести в тетради):
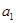 = -0,7614;
= -0,7614; 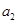 = 1,0305;
= 1,0305; 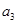 = 0,3747.
= 0,3747.
Уравнение регрессии имеет вид:
У= -0,7614 + 1,0305Х2 + 0,3747Х3.
Далее найдем дисперсии переменных У, Х2 и Х3, а также попарные ковариации этих переменных:
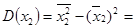 0,085 629 – (0,280 29)2 = 0,007 066;
0,085 629 – (0,280 29)2 = 0,007 066;
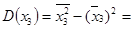 1,187 960 – (1,086 73)2 = 0,006 978;
1,187 960 – (1,086 73)2 = 0,006 978;
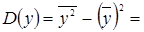 0,007 540 – (-0,065 33)2 = 0,003 272;
0,007 540 – (-0,065 33)2 = 0,003 272;
Cov(Х 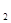 ;У) =
;У) = 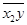 -
- 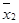 ×
× 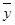 = -0,013 561 1 – 0,280 29 ×(- 0,065 33) = 0,004 750;
= -0,013 561 1 – 0,280 29 ×(- 0,065 33) = 0,004 750;
Cov(Х 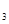 ;У) =
;У) = 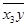 -
- 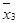 ×
× 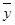 = -0,07 531 85 – 1,086 73 × (- 0,065 33) = -0,004 322;
= -0,07 531 85 – 1,086 73 × (- 0,065 33) = -0,004 322;
Cov(Х 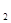 ;Х
;Х 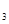 ) =
) = 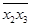 -
- 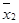 ×
× 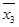 = 0,297 861 – 0,280 29 ×1,086 73 = -0,006 739.
= 0,297 861 – 0,280 29 ×1,086 73 = -0,006 739.
2) Найдем общую дисперсию, объясненную и необъясненную регрессией дисперсии по формулам:
общая дисперсия
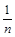
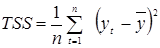 = D(y) = 0,003 272;
= D(y) = 0,003 272;
необъясненная регрессией часть дисперсии
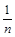
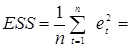
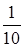 × 0,000 007 24 = 0,000 000 724
× 0,000 007 24 = 0,000 000 724
объясненная регрессией часть дисперсии
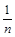
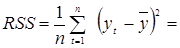
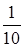 ×0,032 803 = 0,003 280 3
×0,032 803 = 0,003 280 3
3) Найдем коэффициент детерминации
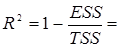 1 -
1 - 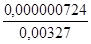 = 0,999 8;
= 0,999 8;
Скорректированный коэффициент корреляции найдем по формуле:
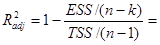 1 -
1 - 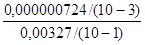 = 0,999 7.
= 0,999 7.
Значение скорректированного коэффициента корреляции близко к единице, значит скорее всего имеется высокая степень линейной зависимости значений У от факторных величин Х 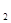 и Х
и Х 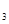 .
.
Однако следует проверить наличие корреляции между факторами Х 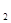 и Х
и Х 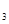 . Для этого найдем частные коэффициенты корреляции.
. Для этого найдем частные коэффициенты корреляции.
4) Сначала найдем коэффициенты корреляции для парных регрессий по формулам:
r 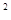 (x2; y) =
(x2; y) = 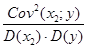 =
= 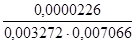 = 0,977 5;
= 0,977 5;
r 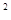 (x3; y) =
(x3; y) = 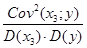 =
= 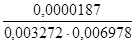 = 0,819 0.
= 0,819 0.
Коэффициент частной корреляции между Уи Х 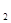 при исключении влияния Х
при исключении влияния Х 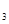 найдем по формуле:
найдем по формуле:
r (у;x2 ½х3) = 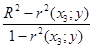 =
= 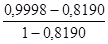 = 0,9989.
= 0,9989.
Коэффициент частной корреляции между Уи Х 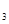 при исключении влияния Х
при исключении влияния Х 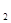 найдем по формуле:
найдем по формуле:
r (у;x3 ½х2) = 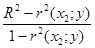 =
= 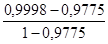 = 0,9911.
= 0,9911.
Коэффициенты частной корреляции близки к единице, значит связь между У и факторами Х 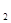 и Х
и Х 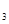 тесная.
тесная.
5) Проверим значимость линейной модели в целом. Для этого на уровне доверия 95% проверим нулевую гипотезу
Н: a2 = a3=0
об отсутствии линейной зависимости между У и факторами Х 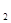 и Х
и Х 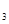 . Для этого рассмотрим F-статистику
. Для этого рассмотрим F-статистику
F = 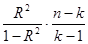 =
= 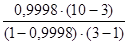 = 17 496,5.
= 17 496,5.
Найдем критическое значение F-статистики:
Fс = F(k-1;n-k) = F(3-1;10-3) = F(2;7)
а) по таблице распределения Фишера при 95% уровне доверия находим
Fc = 4,74
Поскольку F>Fc, то гипотеза Н: a2 = a3=0 с вероятностью 95% отвергается и принимается альтернативная гипотеза о значимости линейной регрессии
6) Найдем доверительные интервалы для параметров регрессии.
Составим матрицу
Q = n× 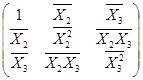 = 10×
= 10× 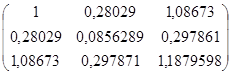
Определитель этой матрицы D = 0, 004
Найдем диагональные элементы матрицы Q-1:
q11 = 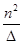 ×(
×(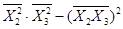 ) =
) = 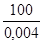 ×(0,101724 – 0,088721) =325,06;
×(0,101724 – 0,088721) =325,06;
q33 = 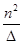 ×(
×(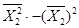 ) =
) = 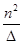 ×D(Х2) =
×D(Х2) = 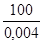 ×0,006 978 = 174,45;
×0,006 978 = 174,45;
q22 = 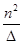 ×(
×(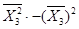 ) =
) = 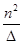 ×D(Х3) =
×D(Х3) = 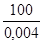 ×0,007 066 = 176,65;
×0,007 066 = 176,65;
Используя t-статистику получим доверительные интервалы для коэффициентов a1, a2, a3
на доверительном уровне 95%:
am Î (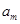 - tc ×
- tc × 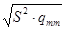 ;
; 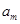 + tc ×
+ tc × 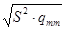 ),
),
где m = 1,2,3.
Критическое значение tc = t(n-k; 0,95) = t(10-3; 0,95) = t(7; 0,95) найдем по таблицам распределения Стьюдента
tc = 2,365;
Несмещенную оценку S2 дисперсии ошибок 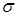 2 найдем по формуле:
2 найдем по формуле:
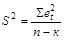 =
= 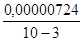 = 0,000 001 03
= 0,000 001 03
Отсюда
tc × 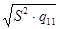 = 0,0434; tc ×
= 0,0434; tc × 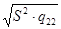 = 0,0320; tc ×
= 0,0320; tc × 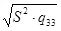 = 0,0318.
= 0,0318.
В результате получим доверительные интервалы на уровне доверия 95%:
a1 Î (-0,7614 – 0,0434; -0,7614 + 0,0434), т.е. a1 Î (-0,8048; -0,7180);
a2 Î (1,0305 – 0,0320; 1,0305 + 0,0320), т.е. a2 Î (0,9985; 1,0625);
a3 Î (0,3747 – 0,0318; 0,3747 + 0,0318), т.е. a3 Î (0,3429; 0,4065).
7) Проверим значимость регрессии. Для этого на уровне значимости 95% проверим гипотезы
Н1: α1= 0; Н2: α2= 0; Н3: α3= 0.
Составим 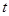 – статистики
– статистики
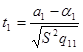 ;
; 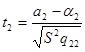 ;
; 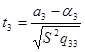
и найдем их значения:
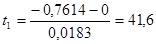 ,
, 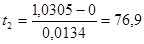 ,
, 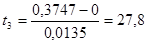
Сравнивая полученные значения 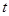 -статистик с критическим
-статистик с критическим 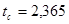 получим, что
получим, что 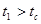 ,
, 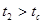 ,
, 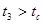 , т.е. все три гипотезы Н1, Н2 и Н3 должны быть отвергнуты на уровне доверия 95% и приняты альтернативные гипотезы, т.е. с вероятностью 95% все три коэффициента α1, α2, α3 значимы.
, т.е. все три гипотезы Н1, Н2 и Н3 должны быть отвергнуты на уровне доверия 95% и приняты альтернативные гипотезы, т.е. с вероятностью 95% все три коэффициента α1, α2, α3 значимы.
8) Проверим наличие мультиколинеарности. Для этого составим матрицу коэффициентов корреляции и найдем ее определитель 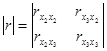 ,
,
где 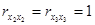 ,
, 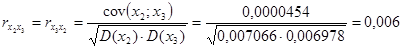
Составленный определитель равен
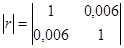 =1-0,000036=0,999964
=1-0,000036=0,999964
На уровне значимости 95% проверим гипотезу о независимости факторных переменных
H: 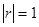
Для этого рассчитаем величину 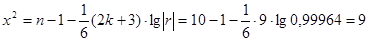
Критическое значение найдем по таблицам распределения 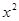 : Пирсона при уровне значимости 95%
: Пирсона при уровне значимости 95%
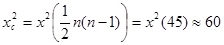
Поскольку 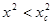 , то гипотеза Н принимается на уровне доверия 95%, т.е. можно считать, что мультиколлинеарности нет.
, то гипотеза Н принимается на уровне доверия 95%, т.е. можно считать, что мультиколлинеарности нет.
 2015-05-18
2015-05-18 457
457








