Решение. В таблице представлено распределение 200 драгоценных изделий по количеству примесей в них Х(%) и стоимости Y (тыс

Задача №9

Пример 1

В таблице представлено распределение 200 драгоценных изделий по количеству примесей в них Х(%) и стоимости Y (тыс. руб):

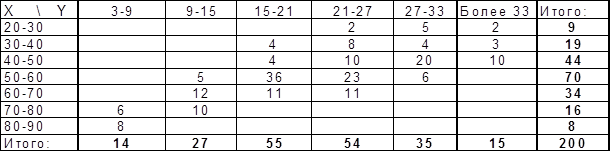
Необходимо:

1. Вычислить групповые средние 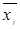и и 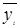построить эмпирические линии регрессии.

2. предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:

а) найти уравнения прямых регрессии и построить их графики на одном чертеже с эмпирическими линиями регрессии;

б) вычислить коэффициент корреляции на уровне значимости 0,05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;

В) используя соответствующее уравнение регрессии, определить количество примесей в драгоценном изделии, если его стоимость составляет 25 тыс. руб.

Решение.

Находим групповые средние по формулам:

; ;

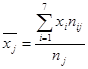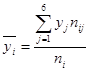, - середины соответствующих интервалов.

=

=

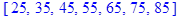
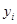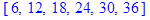
Групповые средние:

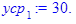
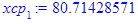
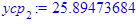
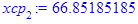
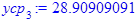
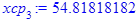
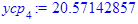
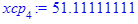
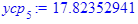
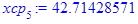
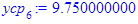
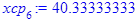
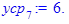
Полученные по формулам значения заносим в таблицу:

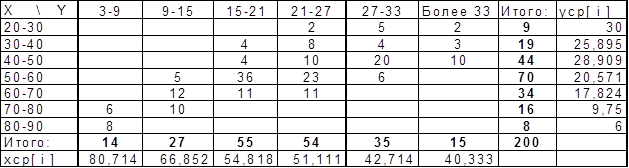
Для нахождения уравнений регрессии вычисляем необходимые суммы:

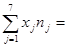25*9+35*19+45*44+55*70+65*34+75*16+85*8 = 10810

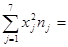
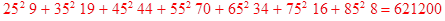
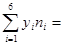6*14+12*27+18*55+24*54+30*35+36*15 =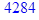

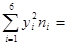
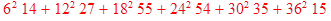
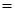
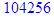
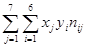= 215580

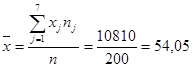
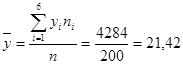
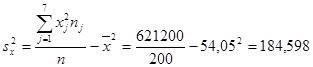
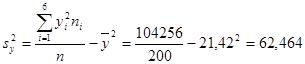
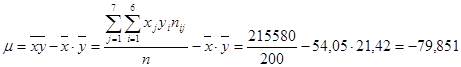
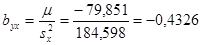
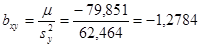
Уравнения прямых регрессии:

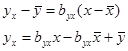
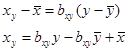
Получаем искомые уравнения регрессии:

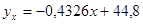
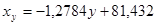
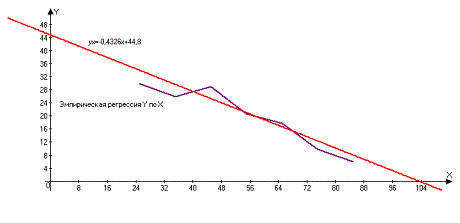
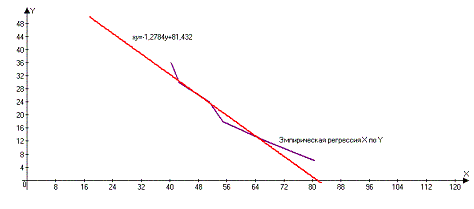
Ниже представлены графики полученных уравнений регрессии совместно с соответствующей эмпирической регрессией

Находим коэффициент корреляции 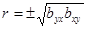радикал берем со знаком -, т.к коэффициенты 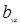и 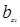отрицательны.

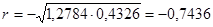
Оценим значимость коэффициента корреляции.

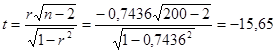
По таблице критерия Стьюдента для уровня значимости 0,05 находим

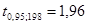
Т.к. 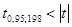, то коэффициент корреляции значимо отличается от нуля. Связь тесная и обратная.

По найденному уравнению регрессии находим:

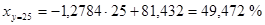
Ответ: Групповые средние:

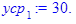
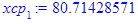
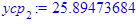
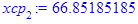
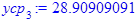
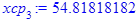
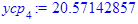
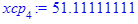
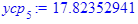
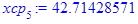
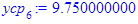
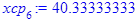
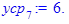
Уравнения регрессии:

Коэффициент корреляции:

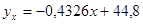
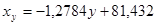
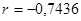
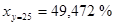
Пример 2. Вычислить выборочный коэффициент корреляции 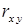, проверить его значимость и найти уравнение линии регрессии.

16,5-19,5	19,5-22,5	22,5-25,5	25,5-28,5	28,5-21,5	31,5-34,5	34,5-37,5
97,5-102,5
102,5-107,5
107,5-112,5
112,5-117,5
117,5-122,5
122,5-127,5
127,5-132,5
132,5-137,5
137,5-142,5

Решение. Найдем условные средние, соответствующие значению 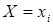, по формуле 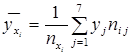. Тогда 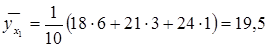; 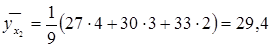и т. д.

Составим корреляционную таблицу

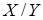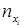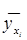									19,5
									29,4
									26,1
									27,6
									29,5
									29,6
									30,7
									30,0
									33,6

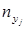Контроль расчетов: 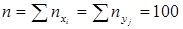- объем выборки.

Для построения эмпирической линии регрессии точки 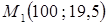, ,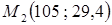…, 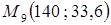соединим ломаной линией.

0

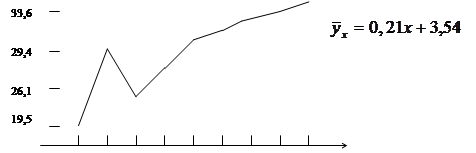
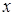
Рис. 7

Для нахождения выборочного коэффициента линейной корреляции 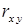найдем

;

.

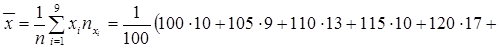
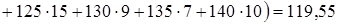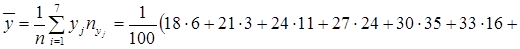
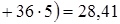Вспомогательно найдем

;

;

.

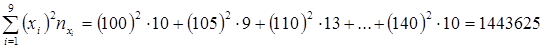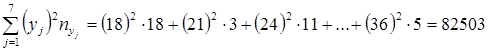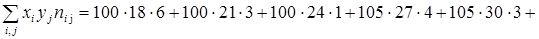
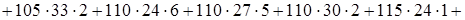
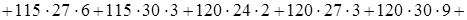
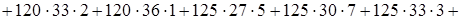
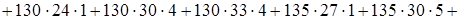
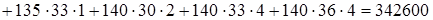Тогда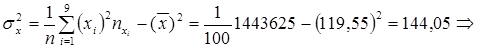

.

.

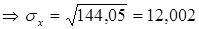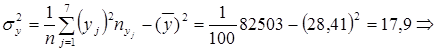
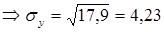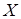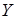Определим ковариацию между и по формуле

.

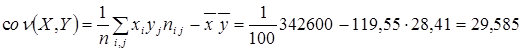Находим коэффициент корреляции по формуле (8):

.

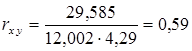Имеем 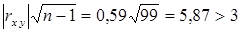, следовательно, связь между случайными величинам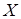и и 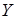достаточно вероятна.

Для проверки значимости коэффициента корреляции проверим нулевую гипотезу 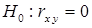; конкурирующая гипотеза .

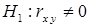Найдем по опытным данным величину

.

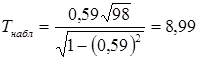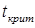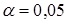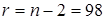
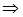
Найдем критическое значение по таблице критерия Стьюдента (прил. 3) при уровне значимости и числе степеней свободы 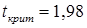. Тогда 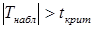, поэтому гипотезу 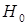отвергаем и принимаем гипотезу 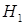, т. е. случайные величины 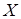и 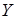коррелированы.

По виду эмпирической линии регрессии можно предположить, что между случайными величинами существует линейная корреляция, т. е. 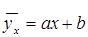. Находим коэффициенты 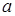и 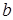по формулам (7):

; .

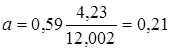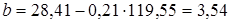Тогда уравнение линейной регрессии

.

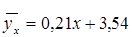Для построения полученной прямой возьмем две точки

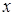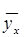	26,4	32,7

График прямой 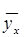достаточно близко расположен по отношению к опытной линии регрессии. Коэффициент корреляции 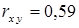показывает, что зависимость между случайными величинам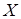и и 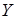заметная и с увеличением значений одной случайной величины значения другой случайной величины имеют тенденцию в среднем увеличиваться.