Нередко экономические задачи имеют не единственное решение и требуется выбрать лучшее – оптимальное из них. Моделирование таких задач сводится к задачам математического программирования (ЗМП).
Математическое программирование – область математики, изучающая оптимизационные процессы посредством поиска экстремума функции при заданных ограничениях.
Сформулируем в общем виде ЗМП:
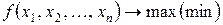 (7)
(7)
при условиях
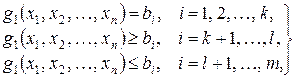 (8)
(8)
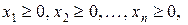 (9)
(9)
где 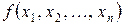 – целевая функция, условия (8) – специальные ограничения, условия (9) – общие ограничения ЗМП.
– целевая функция, условия (8) – специальные ограничения, условия (9) – общие ограничения ЗМП.
Точку 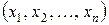 , координаты которой удовлетворяют ограничениям (8) и (9), называют допустимым решением ЗМП.
, координаты которой удовлетворяют ограничениям (8) и (9), называют допустимым решением ЗМП.
Множество всех допустимых решений ЗМП называют допустимым множеством.
Допустимое решение 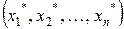 , удовлетворяющее соотношению (7), называют оптимальным решением ЗМП.
, удовлетворяющее соотношению (7), называют оптимальным решением ЗМП.
Если в ЗМП целевая функция 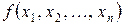 и функции
и функции 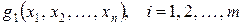 , – линейные, то имеем общую задачу линейного программирования (ЗЛП):
, – линейные, то имеем общую задачу линейного программирования (ЗЛП):
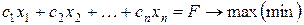 (10)
(10)
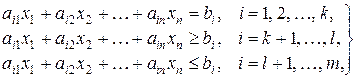 (11)
(11)
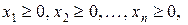 (12)
(12)
В зависимости от вида специальных ограничений различают следующие ЗЛП:
- каноническая ЗЛП, включающая в качестве ограничений (11) только уравнения, т. е.
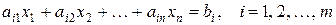 ;
;
- стандартная ЗЛП, включающая в качестве ограничений (11) только неравенства, т. е.
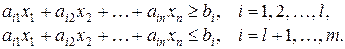
Рассмотрим следующие примеры моделей, приводимых к ЗЛП.
Пример 1. Экономико-математическая модель задачи о планировании производства.
На заводе имеются запасы трех видов сырья: 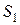 ,
, 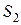 и
и 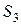 , из которого можно наладить производство двух видов товаров:
, из которого можно наладить производство двух видов товаров: 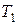 и
и 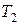 . Запасы сырья, норма его расхода на производство единицы товаров, а также прибыль от реализации единицы каждого товара приведены в таблице 1 (цифры условные).
. Запасы сырья, норма его расхода на производство единицы товаров, а также прибыль от реализации единицы каждого товара приведены в таблице 1 (цифры условные).
Таблица 1
| Сырье Товары | 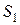
| 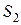
| 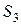
| Прибыль |
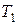
| ||||
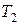
| ||||
| Запасы |
Необходимо составить такой план производства товаров, при котором прибыль от их реализации будет максимальной.
Решение.
План производства зададим числами 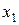 и
и 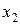 , где
, где 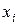 – количество единиц товара
– количество единиц товара 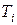 , которое следует произвести
, которое следует произвести 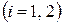 . Неизвестные
. Неизвестные 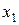 и
и 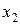 должны удовлетворять условиям
должны удовлетворять условиям
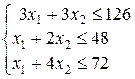 или
или 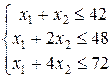 , (13)
, (13)
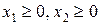 (14)
(14)
Поясним смысл первого неравенства системы (13). В левой части записано количество сырья 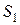 , которое расходуется на выпуск
, которое расходуется на выпуск 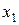 единиц товара
единиц товара 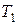 и
и 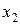 единиц товара
единиц товара 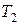 . Это количество не должно превышать имеющегося запаса сырья
. Это количество не должно превышать имеющегося запаса сырья 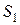 , т. е. 126 единиц. Аналогичный смысл имеют второе и третье неравенства системы (13).
, т. е. 126 единиц. Аналогичный смысл имеют второе и третье неравенства системы (13).
Прибыль, предприятия от реализации плана (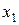 ,
, 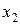 ) производства товаров, очевидно, составит
) производства товаров, очевидно, составит
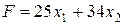 . (15)
. (15)
В интересах предприятия максимизировать эту прибыль. Следовательно, чтобы составить план производства товаров, при котором прибыль от их реализации будет максимальной нужно решить стандартную ЗЛП: 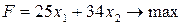 при условиях (13) и (14):
при условиях (13) и (14):
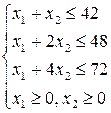
Пример 2. Экономико-математическая модель задачи о диете.
Имеются два вида продуктов: 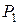 и
и 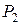 . Содержание в 1 кг питательных веществ A, B и C, ежесуточные потребности организма V в них и стоимость S 1 кг продуктов приведены в таблице 2
. Содержание в 1 кг питательных веществ A, B и C, ежесуточные потребности организма V в них и стоимость S 1 кг продуктов приведены в таблице 2
Таблица 2
| Витамины Продукты | A | B | C | S |
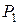
| ||||
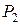
| ||||
| V |
Составить такую ежесуточную диету, которая обеспечивает необходимое количество питательных веществ при минимальных затратах на продукты.
Решение.
Пусть 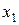 и
и 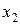 – искомые количества продуктов
– искомые количества продуктов 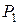 и
и 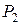 соответственно. Их стоимость составляет
соответственно. Их стоимость составляет
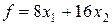
Общее количество питательного вещества A в обоих видах продуктов равно 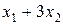 . Оно должно быть не меньше 6 единиц:
. Оно должно быть не меньше 6 единиц: 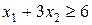 .
.
Аналогичные неравенства составим для питательных веществ B и C: 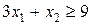 и
и 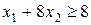 .
.
Очевидно, 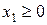 и
и 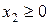 .
.
Таким образом, получим следующую стандартную ЗЛП:
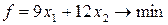 (16)
(16)
при условиях
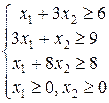 (17)
(17)
 2015-05-18
2015-05-18 620
620








