Определение. СВДТ Х имеет геометрическое распределение, если ее возможные значения (реализации) 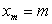 , где
, где 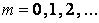 (счетное множество значений), а соответствующие им вероятности выражаются формулой
(счетное множество значений), а соответствующие им вероятности выражаются формулой 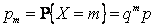 , где
, где 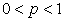 ;
; 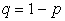 .
.
Вероятности 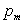 для последовательных значений m образуют геометрическую прогрессию с первым членом p и знаменателем q (отсюда и название – «геометрическое распределение»).
для последовательных значений m образуют геометрическую прогрессию с первым членом p и знаменателем q (отсюда и название – «геометрическое распределение»).
Замечание. Это распределение зависит от одного параметра p, поэтому пишут 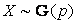 .
.
Геометрическое распределение появляется в следующих условиях. Пусть производится ряд независимых опытов с целью получения какого-то результата («успеха»). При каждом опыте «успех» достигается с вероятностью p. СВ Х – это число «безуспешных» попыток (до первой попытки, в которой появляется «успешный» результат).
Очевидно, что наиболее вероятное значение случайной величины 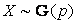 , т.е. мода
, т.е. мода 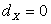 .
.
Важнейшие числовые характеристики случайной величины X, имеющей геометрическое распределение:
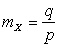 ,
, 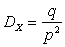 ,
, 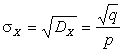 .
.
На практике чаще приходится рассматривать не случайную величину Х, имеющую геометрическое распределение, а другую случайную величину Y –число попыток до первого «успеха», включая удавшуюся. Ряд распределения случайной величины Y имеет вид:
| Y | … | m | … | ||
| P | p | qp | … | 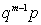
| … |
Такое распределение часто называют «геометрическим, сдвинутым на единицу», или «геометрическим + 1 ».
Очевидно, что наиболее вероятное значение случайной величины Y, т.е. мода 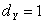 .
.
Важнейшие числовые характеристики случайной величины Y:
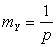 ;
; 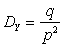 ,
, 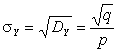 .
.
Пример 2.1.31. Стрелку выдаются патроны до тех пор, пока он не промахнется. Вероятность его попадания в цель при каждом выстреле – 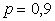 . Какова вероятность того, что он получит не менее трех патронов?
. Какова вероятность того, что он получит не менее трех патронов?
Решение. Пусть случайная величина Х – это количество патронов, которое получит стрелок. Тогда:
| X | … | |||
| P | 0,1 | 0,9×0,1 | 0,92×0,1 | … |
Отсюда 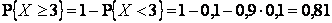 .
.
Ответ: 0,81.
Пример 2.1.32. Вероятность попадания баскетболистом в корзину при штрафном броске равна 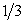 . На тренировке баскетболист выполняет штрафные броски до тех пор, пока не попадет в корзину, а затем передает мяч другому игроку. Пусть X – количество бросков, сделанных баскетболистом. Составить закон распределения случайной величины X, найти ее наиболее вероятное значение (моду),
. На тренировке баскетболист выполняет штрафные броски до тех пор, пока не попадет в корзину, а затем передает мяч другому игроку. Пусть X – количество бросков, сделанных баскетболистом. Составить закон распределения случайной величины X, найти ее наиболее вероятное значение (моду), 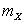 и
и 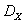 .
.
Решение. Случайная величина X имеет «геометрическое + 1» распределение, в котором 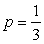 ,
, 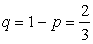 . Тогда закон распределения случайной величины X удобно задать аналитически:
. Тогда закон распределения случайной величины X удобно задать аналитически:
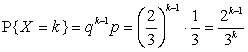 , где
, где 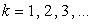 .
.
Наиболее вероятное значение (мода) 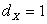 ,
, 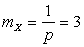 ,
, 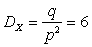 .
.
Ответ: 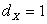 ,
, 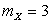 ,
, 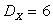 .
.
 2015-05-20
2015-05-20 841
841








