2015-05-20
572
Выделим в покоящейся жидкости элементарный объем в виде параллелепипеда с ребрами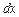 
, 
, 
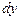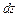(рис. 2.1). Отбросим окружающую жидкость, заменив ее влияние соответствующими силами гидростатического давления (на рис. 2.1). Рассмотрим только величины давлений по оси 
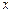). Полагаем, что вдоль оси 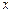слева на грань 
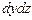действует гидростатическое давление 
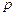, а справа на такую же грань с противоположной стороны действует гидростатическое
давление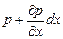 
. Соответственно силы давления составляют на
левую грань -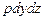 
, на правую грань - 
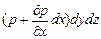. По другим осям координат действуют аналогичные давления.
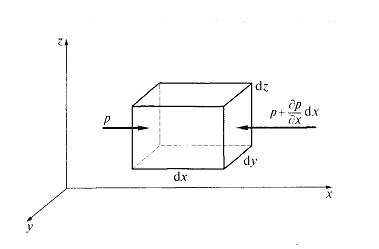
Рисунок 2.1 К оценке сил, действующих на элементарный объем
Помимо сил давления на рассматриваемый параллелепипед действует массовая сила (например, сила тяжести, центробежная сила и др.), проекция которой на координатную ось 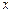будет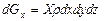 
. Суммируя проекции этих сил на рассматриваемую ось, получим
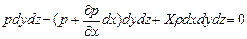, (2.3)
а после раскрытия скобок, сокращений и упрощений, при которых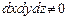 
, имеем:
.
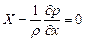Аналогичным образом можно получить уравнения в проекции на ос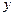и 
и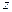 
, и в итоге имеем систему дифференциальных уравнений равновесия жидкости Эйлера:
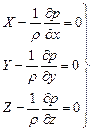. (2.4)
Для установления закономерности изменения давления при изменении координат следует рассмотреть систему уравнений Эйлера (2.4). Умножим первое уравнений системы (2.4) на 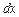, второе на 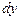, третье на 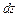и сложим их:
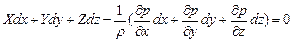(2.5).
Выражение в скобках представляет собой полный дифференциал давления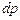 
и, решая это уравнение относительно 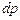, получим:
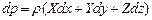, (2.6)
где 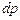- полный дифференциал давления;
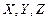- проекции ускорения массовых сил на координатные оси; 
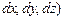- приращения координат.
Уравнение (2.6) называется основным дифференциальным уравнением гидростатики.
