Так как в 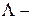 исчислении все функции анонимны (без имен), то необходимо их вызов производить не по имени, а другим способом. Например, рассмотрим рекурсивную функцию, которая в качестве одного из аргументов имеет ссылку на себя:
исчислении все функции анонимны (без имен), то необходимо их вызов производить не по имени, а другим способом. Например, рассмотрим рекурсивную функцию, которая в качестве одного из аргументов имеет ссылку на себя:
а) 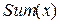 - сложение всех целых чисел:
- сложение всех целых чисел:
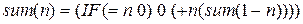 – если
– если 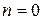 , то
, то 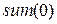 , иначе складываем (+) число
, иначе складываем (+) число 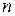 с суммой для числа, меньшего на 1, чем
с суммой для числа, меньшего на 1, чем 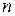 , т.е. (1–) обозначает уменьшение на 1. Это была форма записи рекурсивной функции на языке Гильберта-Клини, а в форме
, т.е. (1–) обозначает уменьшение на 1. Это была форма записи рекурсивной функции на языке Гильберта-Клини, а в форме 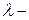 абстракции:
абстракции: 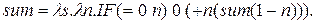 Осталось связать переменную
Осталось связать переменную 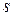 со значением функции
со значением функции 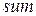 , чтобы сделать функцию анонимной. Это можно сделать с помощью специальной функции «
, чтобы сделать функцию анонимной. Это можно сделать с помощью специальной функции «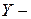 комбинатор»:
комбинатор»:
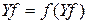 .
.
Например, функция «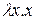 » имеет бесконечное число «неподвижных» точек. Таким образом, в
» имеет бесконечное число «неподвижных» точек. Таким образом, в 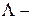 исчислении функция
исчислении функция 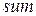 записывается так:
записывается так:
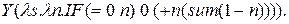
Проверим, например, 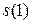 должно быть равно 1.:
должно быть равно 1.:
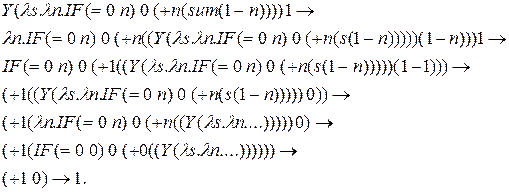
Определим «комбинатор» 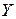 как
как
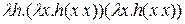 .
.
Проверим выполнение формы записи 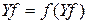 :
:
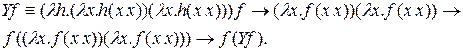
Чистое  исчисление
исчисление
Чистое 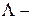 исчисление получается при удалении констант и
исчисление получается при удалении констант и 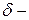 правил, так как в нем любые константы и функции можно построить атомарными термами, использующие только лишь переменные.
правил, так как в нем любые константы и функции можно построить атомарными термами, использующие только лишь переменные.
ПРИМЕРЫ:
а) 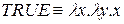 ; б)
; б) 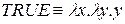 ; в)
; в) 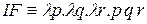 .
.
Легко проверить, что выполняются следующие редукции:
1. 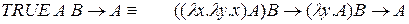
2. 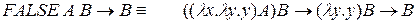
3. 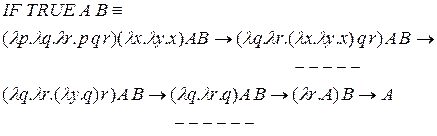
Нумерация Черча: 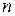 представлять композицией
представлять композицией 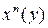 , т.е.
, т.е. 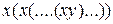 , т.е.
, т.е. 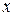 повторяется
повторяется 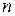 раз. Для каждого натурального
раз. Для каждого натурального 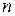 положим:
положим: 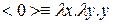 ,
,
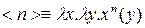 . Тогда «сложение» чисел определяется
. Тогда «сложение» чисел определяется 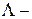 выражением:
выражением:
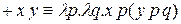 .
.
Проверка: 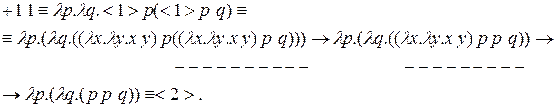
Определение: Говорят, что частичная функция 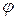 с
с 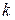 аргументами
аргументами 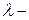 определима термом
определима термом 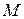 , когда терм
, когда терм 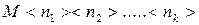
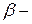 редуцируется к терму
редуцируется к терму 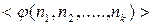 , если значение
, если значение 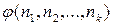 определено, и
определено, и 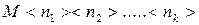 не имеет нормальной формы, если
не имеет нормальной формы, если 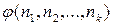 не определено.
не определено.
Теорема Клини: Частичная функция частично-рекурсивна тогда и только тогда, когда она 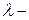 определима.
определима.
 2015-05-20
2015-05-20 491
491








