Алгоритмически Неразрешимые Проблемы (анп)

Определение 1: Предикат 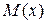называется «разрешимым», если его характеристическая функция, задаваемая формулой: 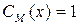, если 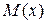– истинно; 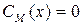, если 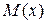– ложно, вычислима.

Определение 2: Предикат 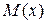называется «неразрешимым», если он не является разрешимым.

Алгоритмически Неразрешимые Проблемы:

1. Теорема Черча «о неразрешимости логики предикатов»: Не существует алгоритма, который для любой формулы логики предикатов устанавливает, общезначима она или нет.

2. Проблема остановки программы неразрешима: Не существует общего алгоритма проверки программ на наличие в них бесконечных циклов, т.е. на языке исчисления: «Не существует общего алгоритма узнать, имеет ли данное выражение «нормальную форму» или нет».

3. Не существует алгоритма установить, что две программы вычисляют одну и ту же одноместную функцию, т.е. универсальное тестирование не возможно.

4. Диофантово полиномиальное уравнение 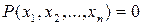имеет или не имеет целочисленного решения? Не существует общего алгоритма, который может установить конкретный ответ (Матиясевич доказал эту теорему).

§ 2.7. Сложность алгоритмов.

Определение: Однородный класс вычислительных задач будем называть «проблемой (массовой задачей)» и обозначать через Т, а алгоритм, ее решающий, через А. Частный случай Т обозначим через 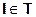. А выполняет последовательность вычислений 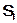. Длина 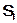характеризует время вычислений. Глубина 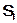- число уровней параллельных шагов – время параллельных вычислений.

1) 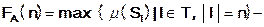сложность вычислений «в наихудшем случае», где 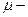мера вычисления может быть выбрана как: а) число элементов или б) глубина или в) число модулей (уровень технологии); 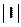– размер.

2) 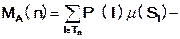сложность «поведения в среднем», где - вероятность появления I среди возможных частных случаев .

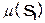3) Анализ алгоритмов связан с вопросом «для заданной функции размера и меры вычисления точно определить для данного алгоритма А, решающего проблему Т, либо сложность 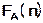«для наихудшего случая», либо, при подходящих предположениях, «поведение в среднем» 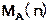. (Кнут «Искусство программирования»).

4) Сложность задачи – сложность наилучшего алгоритма, известного для ее решения (нижняя оценка сложности алгоритма).

Определение: Будем говорить, что функция 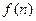есть 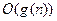, если существует константа с такая, что 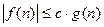для всех натуральных n.

Основной вопрос теории сложности: с какой стоимостью может быть решена заданная проблема?

2.7.1. Классификация задач по степени сложности

а) линейные 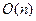; б) быстрее их - 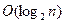; в) полиномиальные алгоритмы принадлежат к классу 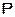, для которых временная сложность порядка 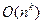, где 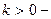целое;

г) экспоненциальные – для них не существует оценки .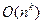

Определение: Задача «труднорешаема», если для нее не существует «полиномиального» алгоритма.

Замечание: для малых 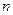«экспоненциальный» алгоритм может быть быстрее полиномиального.

Класс Р:

1) найти эйлеров цикл на графе из 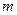ребер: алгоритм проверки циклов - 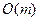; 2) задача Прима-Краскала: 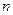городов в плоской стране. Общая длина телефонных линий соединения городов минимальна. Жадный алгоритм находит «остовное» дерево за .

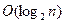3) Быстрое преобразование Фурье (БПФ) за 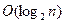шагов; 4) Умножение целых чисел по алгоритму Шенхаге-Штрассена (Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов.-М.: Мир, 1979.-536 с.) за 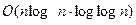шагов по сравнению с умножением двух 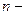разрядных чисел по традиционному алгоритму .

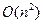5) Умножение матриц - .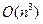

КЛАСС Е:

1) построить множество всех подмножеств; 2) все полные подграфы графа или все поддеревья графа.

ЗАДАЧИ, не принадлежащие к классу Р ине принадлежащие к классу Е:

1) задача «коммивояжера»; 2) задача «составления расписаний при определенных условиях»; 3) задача «оптимальной загрузки емкости (рюкзака, вагонов поезда, самолета и т.д.); 4) задача «распознавания простого числа» и другие.

Определение: Детерминированный алгоритм – алгоритм, в котором переход из одного состояния в другое однозначный. Недетерминированный имеет несколько вариантов перехода (вероятностный переход).

Определение: Класс NP задач, которые решаемы недетерминированными алгоритмами за время 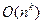, то есть .

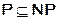Замечание: Так как число путей вычисления может быть экспоненциально, то алгоритмы NP сильнее алгоритмов класса Р.

Замечание: Оптимизация задачи «коммивояжера» - задача класса NP, таккак полиномиального алгоритма пока нет. Алгоритм NP состоит из 2-х стадий: а) стадия угадывания последовательности городов; б) стадия проверки маршрута длины – полиномиальная процедура.