Правило 1: Пусть 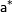 и
и 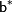 — приближенные значения чисел
— приближенные значения чисел  и
и 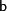 , тогда абсолютная погрешность алгебраической суммы (суммы или разности) не превосходит суммы абсолютных погрешностей слагаемых, т.е.[1]:
, тогда абсолютная погрешность алгебраической суммы (суммы или разности) не превосходит суммы абсолютных погрешностей слагаемых, т.е.[1]:
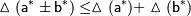
Правило 2: Пусть  и
и 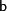 — ненулевые числа одного знака, тогда:
— ненулевые числа одного знака, тогда:
1. 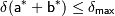 ; 2.
; 2. 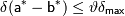 .
.
Здесь 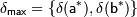 , а
, а 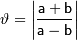 [1].
[1].
Первое из равенств означает, что при суммировании чисел одного знака не происходит потери точности, если оценивать точность в относительных единицах. Совсем иначе обстоит дело при вычитании чисел одного знака. Здесь граница относительной ошибки возрастает в 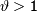 раз и возможна существенная потеря точности. Если числа
раз и возможна существенная потеря точности. Если числа  и
и 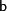 близки настолько, что
близки настолько, что 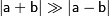 ,то
,то 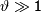 и не исключена полная или почти полная потеря точности. Когда это происходит, говорят о катастрофической потери точности.
и не исключена полная или почти полная потеря точности. Когда это происходит, говорят о катастрофической потери точности.
При построении численного метода решения задачи следует избегать вычитания близких чисел одного знака. Если же такое вычитание неизбежно, то следует вычислять аргументы с повышенной точностью, учитывая ее потерю примерно 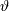 раз.
раз.
Правило 3: Для относительных погрешностей произведения и частного приближенных чисел верны оценки:
1. 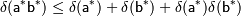 ;
;
2. 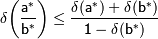 ;
;
в последней из которых 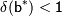 [1].
[1].
Приведенные равенства чаще всего используют для практической оценки погрешности.
Выполнение арифметических операций над приближенными числами, как правило, сопровождается потерей точности. Единственная операция, при которой потеря не происходит, — это сложение чисел одного знака. Наибольшая потеря точности может произойти при вычитании близких чисел одного знака.
 2015-05-20
2015-05-20 1216
1216








