Погрешности элементарных функций

1. Погрешность функции многих переменных

Пусть 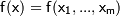— дифференцируемая в области 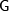функция 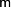переменных, вычисление которой производится при приближенно заданных значениях аргументов 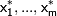, тогда для абсолютной погрешности значения 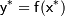справедлива следующая оценка:

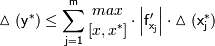
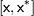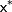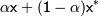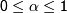Здесь - отрезок, соединяющий точки и : множество точек вида , где ; а .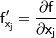

Оценка вытекает из формулы конечных приращений Лагранжа [1].

Для оценки границ относительных погрешностей используют равенство:

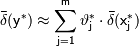
Здесь .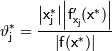

2. Погрешность неявной функции

Нередко приходится сталкиваться с ситуацией, когда функция 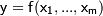задается не явной формулой, а как решение нелинейного уравнения 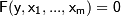, т.е. неявно. Если для такой неявной функции воспользоваться известными формулами вычисления производных:

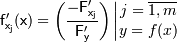то исследование неустранимой погрешности неявной функции сразу же сводится к рассмотренному выше случаю.