Абсолютная и относительная погрешности. Пусть имеется некоторая числовая величина, и числовое значение, которое ей присвоено , считается точным

Пусть имеется некоторая числовая величина, и числовое значение, которое ей присвоено 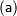, считается точным, тогда под погрешностью приближенного значения числовой величины (ошибкой) 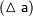понимают разность между точным и приближенным значением числовой величины:

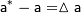
Погрешность может принимать как положительное так и отрицательное значение. Величина 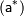называется известным приближением к точному значению числовой величины - любое число, которое используется вместо точного значения. Простейшей количественной мерой ошибки является абсолютная погрешность.

Абсолютной погрешностью приближенного значения 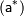называют величину 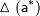, про которую известно, что:

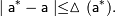
Качество приближения существенным образом зависит от принятых единиц измерения и масштабов величин, поэтому целесообразно соотнести погрешность величины и ее значение, для чего вводится понятие относительной погрешности.

Относительной погрешностью приближенного значения называют величину 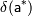, про которую известно, что:

.

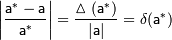Относительную погрешность часто выражают в процентах. Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерения.

Так как точное значение обычно неизвестно, то непосредственное вычисление величин абсолютной и относительной погрешностей по предложенным формулам невозможно. Более реальная и часто поддающаяся решению задача состоит в получении оценок погрешности вида:

(*)

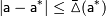
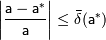где 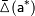и 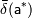— известные величины, которые называют верхними границами (или просто границами) абсолютной и относительной погрешностей.

Если величина 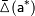известна, то неравенство (*) будет выполнено, если положить

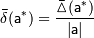
Точно так же если величина 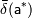известна, то следует положить:

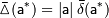
Но поскольку точное значение неизвестно, на практике используют приближенные равенства вида:

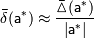
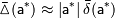
В литературе по методам вычислений широко используется термин "точность". Точное значение величины — это значение, не содержащее погрешности. Повышение точности воспринимается как уменьшение погрешности. Часто используемая фраза "требуется найти решение с заданной точностью " означает, что ставится задача о нахождении приближенного решения, принятая мера погрешности которого не превышает заданной величины . Вообще говоря, следовало бы говорить об абсолютной точности и относительной точности, но часто этого не делают, считая, что из контекста ясно, как измеряется величина погрешности.