-> А - да, В - нет
А - да, В - да
А - нет, В - да
А - нет, В - нет
Дана прямая 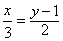
-> угловой коэффициент для этой прямой равен k = 2/3
-> эта прямая пересекает ось ординат в точке y = 1
угловой коэффициент для этой прямой равен k = 2
угловой коэффициент для этой прямой равен k = 3
Запись вектора решений 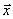 в виде
в виде 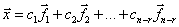 , где векторы
, где векторы 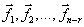 - фундаментальная система решений, а
- фундаментальная система решений, а 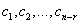 - числовые коэффициенты, представляет собой общее решение _________ системы линей-ных уравнений
- числовые коэффициенты, представляет собой общее решение _________ системы линей-ных уравнений
-> однородной
Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка)
-> Полярные координаты точки P(ρ, φ) <-> пара 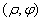 , где
, где 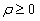 - расстояние от точки до полюса, а
- расстояние от точки до полюса, а 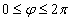 - угол, который образует с полярной осью радиус-вектор точки
- угол, который образует с полярной осью радиус-вектор точки
-> Цилиндрические координаты точки P(ρ, φ, z) <-> тройка чисел 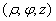 , где
, где 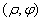 - полярные координаты проекции точки на плоскость Oxy, а z - обычная декартова координата точки P вдоль оси z
- полярные координаты проекции точки на плоскость Oxy, а z - обычная декартова координата точки P вдоль оси z
-> Сферические координаты точки P(r,φ,ψ) <-> тройка чисел 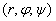 , где r - радиус-вектор точки P, φ - полярная координата проекции точки на плоскость Oxy, а
, где r - радиус-вектор точки P, φ - полярная координата проекции точки на плоскость Oxy, а 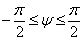 - угол, образованный радиус-вектором точки r и координатной плоскостью Oxy
- угол, образованный радиус-вектором точки r и координатной плоскостью Oxy
У матрицы 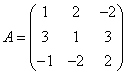
-> определитель равен 0
-> имеются зависимые строки
определитель равен -2
все строки независимы
Даны 4 ряда: А) 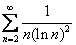 ; В)
; В) 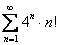 ; C)
; C) 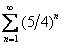 ; D)
; D) 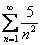 .
.
-> сходимость (расходимость) ряда А может быть определена с помощью интегрального признака Коши-Маклорена
-> ряд В является расходящимся
-> ряд C имеет предел 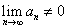
ряд D является расходящимся
Укажите соответствие между терминами (левая колонка) и соответствующими формулами и определениями (правая колонка)
-> Производная сложной функции <-> 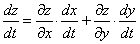
-> Функция  имеет в точке
имеет в точке 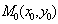 максимум (минимум) <-> существует такая окрестность точки
максимум (минимум) <-> существует такая окрестность точки 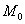 , что для всех точек
, что для всех точек 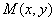 из этой окрестности, отличных от
из этой окрестности, отличных от 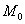 выполняется неравенство
выполняется неравенство 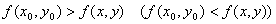
-> Необходимые усло-вия существования экстремума для функции  в точке
в точке 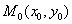 <->
<-> 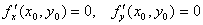
Вычислите дифференциал функции 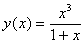
-> 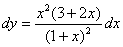
-> 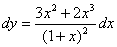
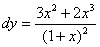
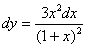
В стандартном базисе задана матрица линейного преобразования 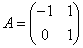 и вектор
и вектор 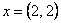 . Координаты образа
. Координаты образа 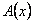 равны
равны
-> (0, 2)
(2, 0)
(1, 1)
(–1, 1)
Достоверное событие - событие
-> которое обязательно произойдет
-> которое обязательно произойдет в эксперименте
-> вероятность которого р = 1
вероятность которого р = 0
вероятность которого 0 <р < 1
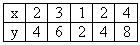
Наблюдения проводились над системой (х, у) двух величин. Результаты наблюдения записаны в таблицу:
 2015-05-20
2015-05-20 472
472








