-> А - нет, В - да
А - да, В - нет
А - да, В - да
А - нет, В - нет
Дифференциальное уравнение 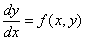 есть
есть
-> дифференциальное уравнение, разрешенное относительно первой производной
дифференциальное уравнение с разделяющимися переменными
линейное дифференциальное уравнение первого порядка
общий вид дифференциального уравнения первого порядка
Установить соответствие между строками в столбцах ниже
-> каноническое уравнение эллипса <-> 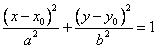
-> каноническое уравнение окружности <-> 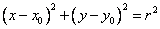
-> каноническое уравнение гиперболы <-> 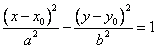
-> каноническое уравнение параболы <-> 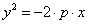
Для решения линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами (например, 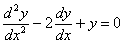 ) сос-тавляется соответствующее ему алгебраическое уравнение (в данном случае
) сос-тавляется соответствующее ему алгебраическое уравнение (в данном случае 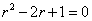 ), которое называется
), которое называется
-> характеристическим
Укажите соответствие между терминами (левая колонка) и соответствующими определениями (правая колонка)
-> Область существования функции двух переменных 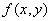 <-> множество
<-> множество 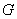 пар значений переменных
пар значений переменных 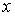 и
и 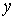 , для которых существует функция
, для которых существует функция 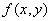
-> Область значений функции двух переменных 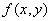 <-> множество всех значений, принимаемых функцией
<-> множество всех значений, принимаемых функцией 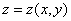 в области определения
в области определения
-> Линия уровня функции 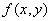 <->
<-> 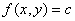
Несмещенная оценка для дисперсии вычисляется по эмпирической дисперсии S2 по формуле: A) 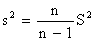 , B)
, B) 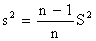 , C)
, C) 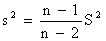 , D)
, D) 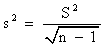
-> A
B
C
D
Даны системы векторов: 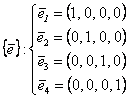
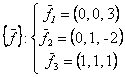 . Базис в R3 образуют системы
. Базис в R3 образуют системы
 2015-05-20
2015-05-20 261
261








