Поверхности и линии уровня

Лекция 1

ТЕОРИЯ ПОЛЯ

Понятие поля лежит в основе многих представлений современной физики. Рассмотрим элементы того математического аппарата, которым приходится пользоваться при изучении физических полей.

В физических задачах чаще всего встречаются величины двух типов: скаляры и векторы. В соответствии с этим мы будем рассматривать два типа полей – скалярные и векторные.

Скалярные поля

Определение и примеры скалярных полей

Пусть W - некоторая область в пространстве. Мы говорим, что в этой области задано скалярное поле, если каждой точке М этой области поставлено в соответствие некоторое число U (М).

Примерами скалярных полей могут служить поле температур внутри некоторого нагретого тела (в каждой точке М этого тела задана соответствующая температура U (М)), поле освещенности, создаваемое каким-либо источником света. и т. д.

Важным примером скалярного поля служит поле плотности массы. Напомним это понятие. Пусть некоторая пространственная область W заполнена непрерывно распределенной массой. Сопоставив каждой области V, содержащейся в W, ту массу, которая находится в области V, мы получим аддитивную функцию области m (V). Если в каждой точке существует производная от m (V) по объему, то эта производная называется плотностью массы, а значения этой производной образуют скалярное поле, называемое полем плотности массы. Аналогично, рассматривая некоторое непрерывное распределение зарядов по пространственной области W, мы приходим к скалярному полю плотности электрического заряда. Число подобных примеров можно было бы увеличить.

Наряду с полями, заданными в пространственных областях, часто приходится рассматривать и плоские скалярные поля. Примером такого поля может служить освещенность части плоскости, создаваемая каким-либо источником света.

Поверхности и линии уровня.

Если U (М) - некоторое скалярное поле, то, введя в области, где задано поле, декартовы координаты можно представить это поле в виде функции U (х, у, z) координат точки М. Эту функцию мы всегда будем в дальнейшем предполагать непрерывной и имеющей в рассматриваемой области непрерывные частные производные первого порядка по х, у и z.

Задание скалярного поля с помощью фиксированной системы координат и соответствующей функции U (х, у, z) не всегда дает достаточно ясное представление о поведении этого поля. Для получения более наглядной картины, удобно пользоваться так называемыми поверхностями уровня. Поверхностью уровня скалярного поля U (М) называется геометрическое место точек, в которых поле U (М) имеет данное фиксированное значение С. Уравнение поверхности уровня имеет вид:

U (х, у, z) = C. (1)

Ясно, что поверхности уровня (отвечающие различным С) заполняют всю область, в которой определено поле, и никакие две поверхности

U (М) = C ₁ и U (М) = C ₂

не имеют общих точек. Задание всех поверхностей уровня с отметкой на них соответствующих значений С равносильно заданию самого поля U (М). Взаимное расположение поверхностей, уровня в пространстве, дает наглядное представление о соответствующем скалярном поле.

Указанный способ изображения поля особенно удобен тогда, когда речь идет о поле, заданном, не в пространственной, а в плоской области. Такое поле описывается функцией двух переменных U (х, у). Равенство вида U (х, у) = С определяет, вообще говоря, некоторую кривую. Такие кривые называются линиями уровня плоского скалярного поля U (М). С помощью линий уровня обычно изображается рельеф местности на топографических картах, а именно, на них проводятся линии, состоящие из точек, имеющих одну и ту же высоту над уровнем моря; эти линии называются горизонталями (рис. 1). Распределение температур, давлений, количества осадков и т. п. обычно также изображается на специальных картах с помощью соответствующих линий уровня (называемых изотермами в случае температур, изобарами, когда речь идет о давлениях, и т. д.).

1.1.3. Различные типы симметрии полей.

Во многих физических задачах приходится иметь дело с полями, обладающими теми или иными специальными свойствами симметрии, облегчающими изучение таких полей. Укажем некоторые частные случаи.

а) Плоскопараллельное поле.

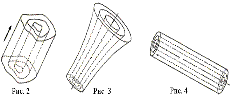
Если скалярное поле U (М) в какой-либо декартовой системе координат можно описать функцией, зависящей не от трех, а только от двух координат, скажем, функцией вида U (х, у), то такое поле называется плоскопараллельным (или двумерным). Иначе говоря, поле U (М) называется плоскопараллельным, если в пространстве существует направление, при сдвигах вдоль которого поле U (М) переходит само в себя. Поверхности уровня такого поля - это семейство цилиндрических поверхностей (рис. 2), в соответствующим образом выбранной системе координат они задаются уравнениями вида

U (х, у) = С.

б) Осесимметрическое поле.

Если для поля U (М)можно подобрать такую цилиндрическую систему координат, в которой оно изображается функцией, зависящей только от переменных 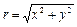и z (но не от угла j), то это поле называется осесимметрическим. Иначе говоря, поле U (М) осесимметрическое, если оно переходит само в себя при повороте пространства (на произвольный угол) вокруг некоторой фиксированной прямой - оси симметрии этого поля.

Поверхности уровня такого поля представляют собой, очевидно, поверхности вращения (рис. 3). Если эти поверхности вращения - круглые цилиндры (рис. 4) т.е. если поле U (М) в соответствующей цилиндрической системе координат изображается функцией, зависящей лишь от одной координаты r (расстояния точки от оси симметрии поля), то U (М) называется цилиндрическим полем.

в) Сферическое поле.

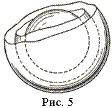
Если значения U (M) зависят лишь от расстояния точки М от некоторой фиксированной точки М ₀, то такое поле называется сферическим. Поверхности уровня сферического поля семейство концентрических сфер (рис. 5).