Распределения случайной величины

КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Функция распределения и плотность

распределения случайной величины

Количественный анализ надежности осуществляется с помощью методов теории вероятностей и математической статистики, предназначенных для изучения случайных величин и событий. Именно случайность является характерной особенностью проблем, возникающих при изучении надежности. Случайными являются моменты возникновения отказов, продолжительность безотказной работы изделий и т.п. Для конкретности под случайной величиной будем понимать продолжительность безотказной работы (ресурс) изделия.

Случайной величиной называют переменную величину, которая в результате опыта может принимать различные значения. Случайные величины обычно обозначают большими буквами, например, Х. Значения случайной величины, которые она принимает в результате опыта, обозначают малыми буквами 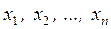. При массовых испытаниях каждое из возможных значений случайной величины 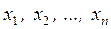может встретиться m ₁, m ₂ ,…,m_n раз. Эти числа называют частотами. Весь набор значений случайной величины называют генеральной совокупностью N _x. Отсеянные из генеральной совокупности N _xзначения грубых ошибок образуют выборку объема N. Если всего было проведено N _x испытаний, то в результате выборки получаем 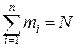, и отношение m_i/N называют частостью или относительной частотой.

Случайные величины бывают дискретными и непрерывными.

Дискретными случайными величинами называют такие, которые могут принимать конечное и счетное множество возможных значений, например: 0,1; 0,2; 0,3 и т.д. К дискретным случайным величинам относится и формула Бернулли для определения вероятности:

P_m,n =C_n^m P^m Q^n-m = 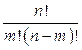P^m Q^n-m ,

где n - количество опытов; m = 0, 1, 2, … – количество событий; Q =1- P.

Пример 1.1. Известно, что вероятность Р безотказной работы изделия при каждом испытании равна 0,8. Проводят n = 10 испытаний. Найти вероятность того, что из 10 испытаний m (m = 2) испытаний будут успешными.

Решение. Для нахождения вероятности воспользуемся формулой Бернулли:

Р _2,10 =С₁₀² ∙0,8²(1 - 0,8)⁸ = 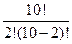∙0,8² ∙0,2⁸=0,00073.

Полученное значение дает 0,073%-ную вероятность.

В технических приложениях наиболее часто встречаются распределения дискретных случайных величин по биноминальному закону и по закону Пуассона (закону редких событий).

Биноминальный закон распределения встречается при повторении испытаний. Если n раз производятся независимые одинаковые опыты, причем вероятность повторения изучаемого события в каждом опыте постоянна и равна P, а вероятность его непоявления Q =1– P, тогда вероятность появления данного события точно x_i раз определится по формуле

.

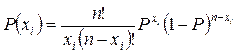Распределение обладает следующими свойствами:

· область значений – целые положительные числа от 0 до n;

· вероятность P может иметь любое значение между 0 и +1;

· при P = 1/2 закон распределения симметричный;

· N – целое положительное число;

· среднее значение 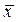= n∙P;

· среднеквадратическое отклонение .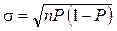

Распределение по закону Пуассона встречается в задачах о повторении испытаний, в которых вероятность ожидаемого события очень мала. В технике это распределение применимо при определении числа редких компонентов на единицу площади или объема, числа атмосферных помех при радиопередачах, при расчете количества запасных частей, определении вероятности восстановления сложных систем и т.п. Закон распределения Пуассона имеет вид:

,

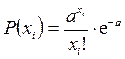где а – параметр распределения; х_i = 0, 1, 2, ….

Свойства распределения:

· распределение несимметричное;

· несимметричность особенно сильно выражена при малых значениях а;

· среднее значение ;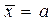

· среднее квадратическое отклонение .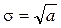

Непрерывными случайными величинами называют такие, которые в некотором интервале могут принимать любое значение. Число бракованных изделий в различных выборках из генеральной совокупности есть дискретная случайная величина, а размер этих изделий – непрерывная случайная величина.

Всякую непрерывную случайную величину можно задать в виде дискретной, если все возможные ее значения разбить на интервалы и задать вероятности появления этих интервалов (из-за ограниченности измерительных средств все замеры непрерывных величин задаются в дискретном виде). Случайные величины характеризуются функциями распределения вероятностей.

Кроме случайной, на практике приходится иметь дело и с систематической величиной. Это такая величина, которая остается постоянной или закономерно изменяется при повторных измерениях одного и того же физического параметра. Она может возникнуть, например, из-за неправильного монтажа устройства или из-за постоянного внешнего воздействия (нагрев, вибрация и т.д.). Систематическая величина может быть исключена путем введения поправки, равной по величине и обратной по знаку погрешности.

Рассмотрим описание распределения случайных величин. Если X – случайная величина, а x – некоторое ее значение, то вероятность Р того, что случайная величина X не превысит значения x, т.е. попадет в интервал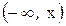

F (x) = P (X< x),

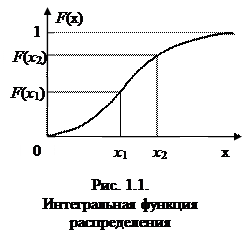где F (x) – интегральная функция распре­деле­ния (рис. 1.1.), определяющая вероят­ность того, что случайная величина примет значения, не превосходящие х_i.

Ее задание и определяет закон распределения случайной величины Х. В общем случае функция распределения F (x) может быть как разрывной, так и непрерывной. Конкретные виды функции распределения для некоторых важных распределений будут рассмотрены ниже.

В большинстве практически важных случаев распределение недискретных случайных величин может быть задано в другой форме с помощью введения функции плотности вероятностейf (x).

Характерной особенностью случайной величины является то, что заранее не известно, какое из значений она примет. Возможность принятия случайной величиной Х значения из элементарного интервала (х ₁, х ₂) количественно оценивается вероятностью

P (x ₁ <X 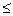x ₂) = f (x)dx, (1.1)

где P (x ₁ <X 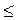x ₂) – вероятность указанного события (x ₁<X 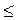x ₂); f (х) - плотность распределения случайной величины; x ₂= x ₁+dх.

Плотность f (х) является важнейшей характеристикой, задающей распределение случайной величины. Плотность удовлетворяет двум условиям: она неотрицательна и интеграл от нее в полных пределах изменения аргумента х равен единице:

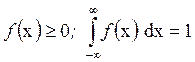. (1.2)

Как видно из формулы (1.1), функция распределения F (х) выражается через плотность f( х ):

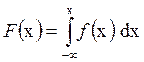. (1.3)

С другой стороны, если плотность f (х) непрерывна в точке х, то ее значение в этой точке равно производной от функции F (х):

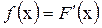. (1.4)

При этом предположении функция распределения F (x)будет являться первообразной для плотности f (x). Поэтому

,

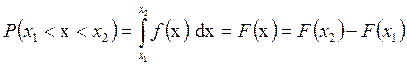f (x)называют также дифференциальной функцией распределения.

Из свойств плотности f (x) и определения функции 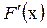следует, что последняя – неотрицательна, не убывает и равна 0 и 1 при значении аргумента

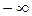и :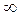

F (х) 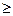0; F (х ₁) 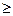F (х ₂)при x ₁ >х ₂; F (– 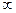) = 0; F (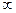) = 1.

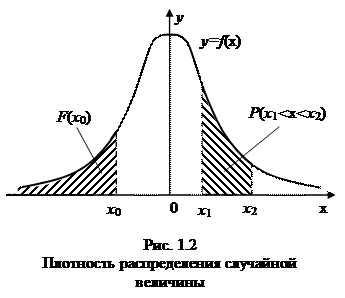
График плотности распределения f (x)называется кривой распределения случайной величины. Исходя из геометрической интерпретации интеграла как площади соот­вет­ствующей криволинейной тра­пеции заключаем, что для произвольного 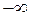< х ₀<+ 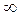чис­ло F (x ₀)равно площади под кривой распределения, лежащей левее прямой х =х ₀. Аналогично интерпретируется вероятность P (x ₁ < x 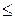x ₂)(рис.1.2).

Случайная величина x, для которой существует плотность распределения f (x), называется непрерывной.

Если под случайной вели­чи­ной X понимать продолжи­тель­ность безотказной работы объек­та, то произведение f (х)dх есть вероятность отказа объекта в интервале времени (х ₁, х ₂).Значение функции распределения F (х) равно вероятности отказа объекта до момента х. В теории надежности часто употребляют такое понятие, как вероятность безотказной работы Р (х), которое является дополнительным понятием к функции распределения F (x).

Значение вероятности безотказной работы в точке х равно вероятности того, что случайная величина X превыситх, т. е. изделие будет работать безотказно в течение времени x:

Р (х) = 1– F (х)= P { X> х}.

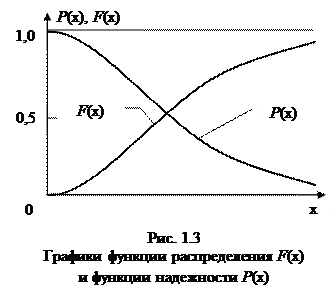Функция Р (х) называется также функцией надежности. Примерные графики функции распределения F (х)и функции надежности Р (х)изображены на рис. 1.3.

На практике часто распо­ла­гают дополнительной инфор­мацией о том, что случайная величина превысила некоторое значение х(в частности, это из­де­лие проработало время xи не отказало).

Разумеется, эта информация изменяет возможность принятия случайной величиной тех или иных значений. В связи с этим вводят специальную функцию - интенсивность отказов 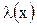. Значение интенсивности отказов в точке х, умноженное на d х, равно вероятности принятия случайной величиной значения из элементарного интервала (х ₁, х ₂) при условии, что эта случайная величина X больше х:

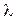(х)dx = P {x < X 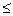x + dx|X > x},

где символ «|» означает «при условии, что…».

В нашем контексте 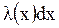есть вероятность отказа изделия сразу после момента времених, если оно до этого не отказало.