Начальные и центральные моменты

Чтобы характеризовать случайные погрешности, часто пользуются некоторыми числовыми вероятностными характеристиками случайных погрешностей, которые называют начальным и центральным моментами. Моменты представляют собой некоторые средние значения и называются начальными, если усредняются величины, отчитываемые от начала координаты, и центральными – от центра функции плотности вероятности.

Первый начальный момент функции распределения плотности вероятностей совпадает с математическим ожиданием результатов наблюдений:

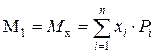. (1.15)

Первый центральный момент результатов наблюдений равен нулю.

Значение стандартного отклонения σносит название второго центрального момента распределения относительно математического ожидания (среднего арифметического значения) случайной величины. Второй центральный момент (дисперсия результатов наблюдений) определяется как

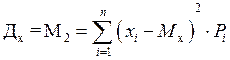. (1.16)

В общем случае момент дискретной случайной величины r -го порядка можно представить в виде

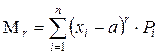, (1.17)

где а – постоянная величина.

Если а = 0, то момент называют начальным, если а = М _хили а = 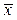× r – центральным. Нечетные центральные моменты указывают на симметрию распределения относительно математического ожидания. У всех симметричных распределений нечетные моменты относительно среднего значения равны нулю.

Для более подробного описания распределения используются моменты более высоких порядков.

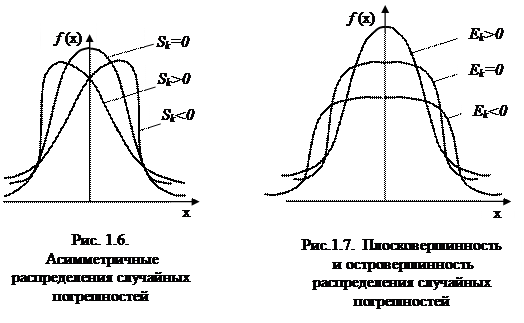
Третий центральный момент (М₃) характеризует асимметрию распределения случайных погрешностей, т.е. скошенность (см. рис. 1.6.).

Асимметрия может оцениваться коэффициентом асимметрии:

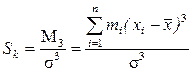. (1.18)

При S_k < 0 наблюдается левосторонняя, а при S_k > 0 – правосторонняя асимметрия данных.

Четвертый центральный момент (М₄) характеризует форму (крутизну кривой), плосковершинность или островершинность распределения случайных

погрешностей (см. рис. 1.7). Крутизна кривой описывается с помощью эксцесса:

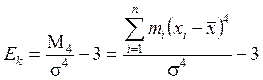. (1.19)

Число 3 вычитают потому, что для нормального распределения погрешностей M₄ = 3, следовательно, E_k = 0, т.е. в качестве кривой с нулевым эксцессом принята кривая нормального распределения.

Выражение 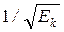называется контрэксцессом. Если E_k > 0, то говорят, что имеется положительный эксцесс, т.е. вершина кривой находится выше кривой нормального распределения. Если E_k < 0 – имеется отрицательный эксцесс и вершина кривой находится ниже вершины кривой нормального распределения.

В случаях, когда значения случайной величины x_i заданы трех- и более значимыми числами и объем выборки N > 25, расчет параметров целесообразно вести путем введения случайной величины

,

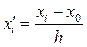где 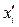– новая случайная величина; h – величина интервала; х ₀ – некоторое начальное значение (обычно принимают середину средних значений x_i).

Рассмотренные числовые характеристики являются основными. Конечная цель при исследовании распределения случайной величины – установление уравнения кривой распределения.