2015-05-20
608
Пусть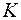 
– код упорядоченного корневого дерева 
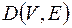. Обозначим через 
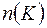– число нулей, 
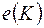– число единиц в коде, 
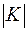– общее число символов. Пусть 
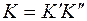, где 
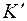и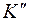 
два подслова. Тогда
а)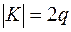 
, где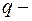 
число ребер в дереве 
;
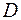б)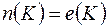 
;
в)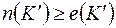 
, причем равенство достигается только тогда, когда 
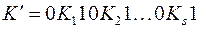, где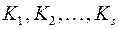 
– коды первых 
поддеревьев дерева .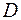
Доказательство. Доказательство проведем по индукции по построению дерева .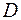
1. Если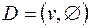 
, то его кодом является пустое слово, число ребер так же равно нулю и все утверждения леммы становятся тривиальными.
2. Пусть дерево 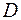имеет поддеревья 
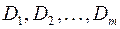и для их кодов 
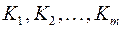все утверждения леммы справедливы.
3. Покажем, что они справедливы для кода дерева 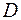. Пусть 
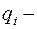число ребер в поддереве 
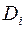, тогда число ребер в дереве 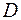будет равно 
.
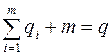а)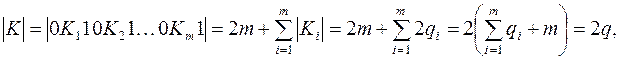 
так как по индуктивному предположению 
.
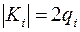б) По индуктивному предположению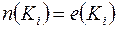 
, при построении кода 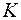добавляется равное число нулей и единиц, отсюда .
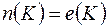в) Если 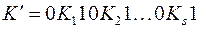, то очевидно, 
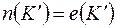. Пусть 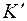имеет вид: 
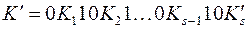, то есть 
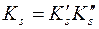. Найдем в этом случае 
. 
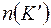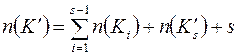, здесь 
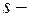количество 0, и 
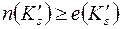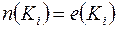, по индуктивному предположению, тогда
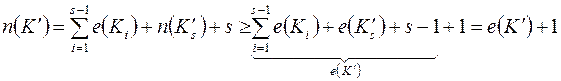, то есть 
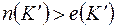, что и требовалось доказать.
Последнее утверждение позволяет в коде дерева выделить коды отдельных поддеревьев. Для этого надо найти точки, где количество нулей совпадает с количеством единиц, то есть надо найти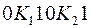 
и т.д. Затем в каждом 
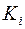проделать такую же процедуру. Таким образом, по коду упорядоченного корневого дерева можно восстановить само дерево.
