2015-05-20
3236
Из любого связного графа можно выделить остовное дерево.
Доказательство. Пусть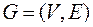 
– связный граф, если в нем нет циклов, то он сам дерево. Пусть граф 
содержит цикл 
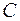. Возьмем ребро 
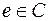, рассмотрим граф 
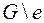, граф 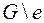– связный (по лемме об удалении ребра из цикла), но количество циклов в нем уменьшилось, по крайней мере на 1. Повторяя эту процедуру до тех пор, пока не разрушатся все циклы, мы получим связный граф без циклов – остовное дерево графа .
Теорема Кирхгофа (1847 г.)
Число остовных деревьев в связном графе порядка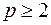 
равно алгебраическому дополнению любого элемента матрицы Кирхгофа.
Пример 6. Рассмотрим граф на рис. 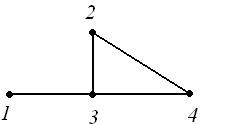18.
Рис. 18
|
Матрица Кирхгофа для этого графа имеет вид
.
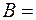
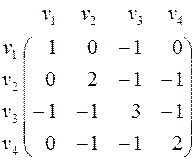Найдем алгебраическое дополнение элемента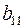 
.
.
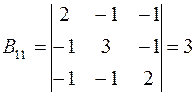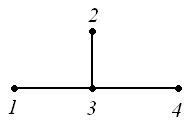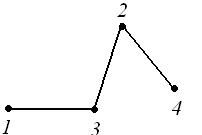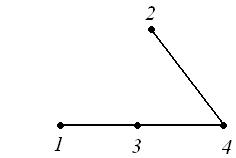Действительно, у графа 3 остовных дерева (рис. 19).
  
Рис. 19
|
Если вершины графа помечены, то все 3 остовных дерева различны. Если вершины не помечены, т.е. занумерованы произвольным образом, то второй и третий граф изоморфны. Теорема Кирхгофа дает число остовных деревьев для графов с помеченными вершинами.
|
|
|
