Перепишем условия (9) следующим образом:
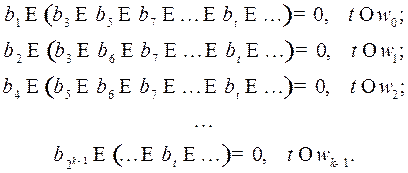 (10)
(10)
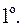 Так как разряды
Так как разряды 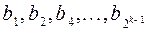 попадают только в одно из множеств
попадают только в одно из множеств 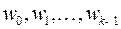 , то они однозначным образом находятся из уравнений (10).
, то они однозначным образом находятся из уравнений (10).
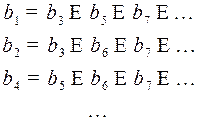 (11)
(11)
Разряды – степени числа 2 называются контрольными, их  , остальные
, остальные 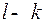 разряды называются информационными. Информационные разряды заполняются произвольным образом, формируя множество кодовых слов, их будет
разряды называются информационными. Информационные разряды заполняются произвольным образом, формируя множество кодовых слов, их будет 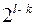 , контрольные разряды вычисляются по информационным в соответствии с уравнениями (11).
, контрольные разряды вычисляются по информационным в соответствии с уравнениями (11).
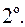 Найдем число контрольных разрядов, если длина кодового слова равна
Найдем число контрольных разрядов, если длина кодового слова равна 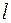 .
.
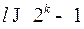 или
или 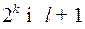 , где
, где  минимальное натуральное число, удовлетворяющее этому неравенству. Это условие можно записать следующим образом:
минимальное натуральное число, удовлетворяющее этому неравенству. Это условие можно записать следующим образом:
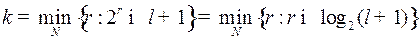 ,
,
что, по определению, означает
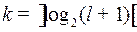 .
.
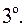 Докажем, что код Хэмминга исправляет одну ошибку типа замещения.
Докажем, что код Хэмминга исправляет одну ошибку типа замещения.
Пусть 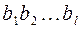 посланное кодовое слово, принадлежащее коду Хэмминга,
посланное кодовое слово, принадлежащее коду Хэмминга, 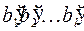 это же слово, полученное при передаче, и пусть ошибка произошла в
это же слово, полученное при передаче, и пусть ошибка произошла в 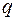 -том разряде:
-том разряде:
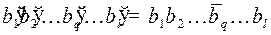 .
.
Исправить ошибку означает установить номер разряда с ошибкой, то есть найти, чему равно 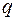 .
.
По полученному слову 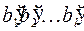 найдем числа
найдем числа 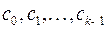 :
:
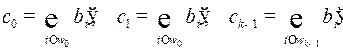 ,
,
где 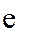 – сумма по модулю
– сумма по модулю 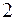 .
.
Утверждается, что число 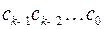 – двоичный код числа
– двоичный код числа 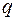 .
.
Действительно, пусть 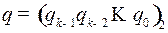 , покажем, что
, покажем, что 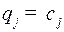 .
.
Пусть 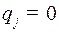 , тогда число
, тогда число 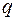 , то есть номер разряда с ошибкой, не входит в множество
, то есть номер разряда с ошибкой, не входит в множество 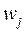 и
и
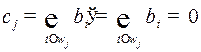 .
.
Пусть 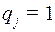 , тогда число
, тогда число 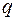 (номер разряда с ошибкой) входит в множество
(номер разряда с ошибкой) входит в множество 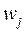 и
и 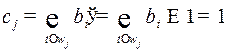 .
.
Таким образом, 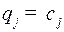 и номер разряда с ошибкой
и номер разряда с ошибкой 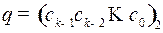 .
.
Пример 9. Построить код Хэмминга для кодирования 10 букв 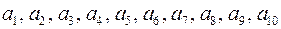 .
.
Решение. Найдем число информационных разрядов для кодирования 10 букв. Их, очевидно, должно быть 4: 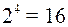 , но трех информационных разрядов недостаточно, так как
, но трех информационных разрядов недостаточно, так как 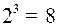 . Информационными разрядами будут
. Информационными разрядами будут 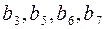 , контрольными разрядами будут
, контрольными разрядами будут 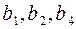 , что согласовывается с формулой
, что согласовывается с формулой 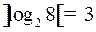 . Длина кодового слова равна 7, все числа от 1 до 7 кодируются трехразрядными двоичными кодами
. Длина кодового слова равна 7, все числа от 1 до 7 кодируются трехразрядными двоичными кодами 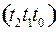 . Дальше осталось произвольным образом заполнить информационные разряды и найти по формулам (11) контрольные (табл. 27).
. Дальше осталось произвольным образом заполнить информационные разряды и найти по формулам (11) контрольные (табл. 27).
Таблица 27
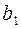
| 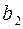
| 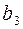
| 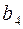
| 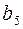
| 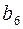
| 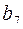
| |
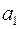
| |||||||
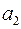
| |||||||
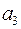
| |||||||
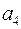
| |||||||
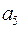
| |||||||
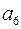
| |||||||
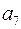
| |||||||
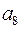
| |||||||
| |||||||
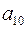
|
Буква 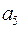 закодировалась словом 0010110, пусть при передаче произошла ошибка в пятом разряде, то есть
закодировалась словом 0010110, пусть при передаче произошла ошибка в пятом разряде, то есть 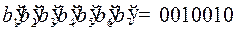 . Найдем номер разряда с ошибкой по полученному слову.
. Найдем номер разряда с ошибкой по полученному слову.
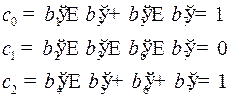
Номер разряда с ошибкой равняется 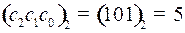 .
.
Часто даются кодовые слова некоторого равномерного кода, состоящие только из информационных разрядов, которые надо закодировать кодом Хэмминга.
Пример 10. Пусть 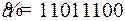 – кодовое слово, состоящее из информационных разрядов. Заполним все разряды, не являющиеся степенями числа 2, для контрольных разрядов оставим свободные места; число их, а также длина слова найдутся автоматически:
– кодовое слово, состоящее из информационных разрядов. Заполним все разряды, не являющиеся степенями числа 2, для контрольных разрядов оставим свободные места; число их, а также длина слова найдутся автоматически:
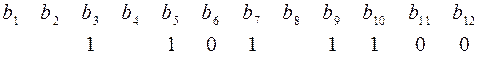 .
.
Контрольными разрядами оказались 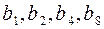 . Числа от 1 до 12 кодируются четырехзначными двоичными кодами и образуют 4 подмножества:
. Числа от 1 до 12 кодируются четырехзначными двоичными кодами и образуют 4 подмножества: 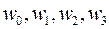 .
.
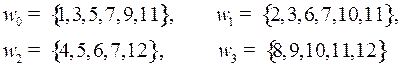
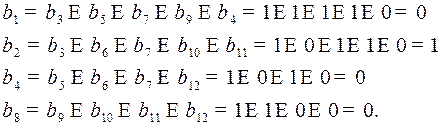
Заполнив контрольные разряды, получим кодовое слово в коде Хэмминга:
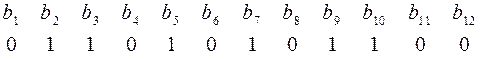 .
.
Пример 11. Пусть 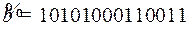 – кодовое слово, закодированное кодом Хэмминга, полученное в процессе передачи. Найдем номер разряда с ошибкой, если ошибки нет, то метод Хэмминга даст в качестве такого номера 0.
– кодовое слово, закодированное кодом Хэмминга, полученное в процессе передачи. Найдем номер разряда с ошибкой, если ошибки нет, то метод Хэмминга даст в качестве такого номера 0.
Решение. Длина слова равна 14, все числа от 1 до 14 кодируются четырехразрядными двоичными кодами 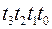 и образуют 4 подмножества:
и образуют 4 подмножества:
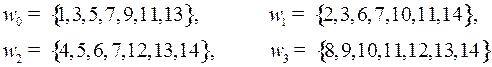
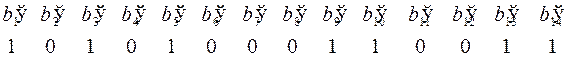 ,
,


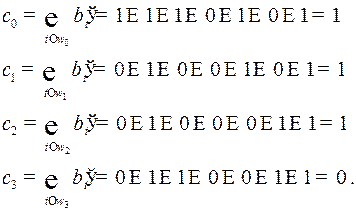
Номер разряда с ошибкой 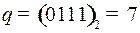 , следовательно,
, следовательно, 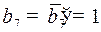 , было послано слово
, было послано слово
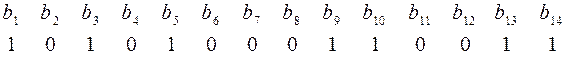 ,
,
уберем из него все контрольные разряды, найдем кодовое слово, состоящее только из информационных разрядов: 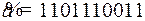 .
.
 2015-05-20
2015-05-20 695
695








