Код суффиксный, нет дуги входящей в вершину 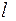 , следовательно, однозначно декодируемый. Граф
, следовательно, однозначно декодируемый. Граф 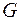 показан на рис. 57.
показан на рис. 57.
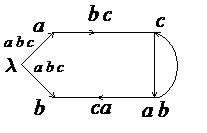
Рис. 57
2. Выяснить, является ли код 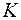 с кодирующим алфавитом
с кодирующим алфавитом 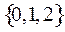 однозначно декодируемым:
однозначно декодируемым:
2.1. 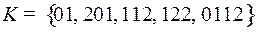 ;
;
2.2. 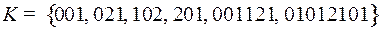 ;
;
2.3. 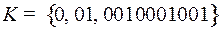 ;
;
2.4. 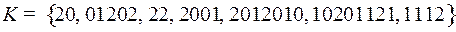 ;
;
2.5. 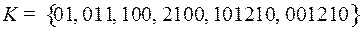 ;
;
2.6. 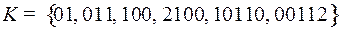 ;
;
2.7. 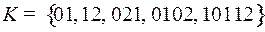 ;
;
2.8. 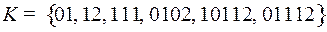 ;
;
2.9. 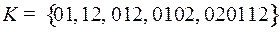 ;
;
2.10. 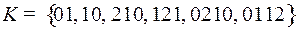 ;
;
2.11. 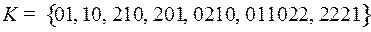 ;
;
2.12. 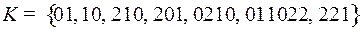 ;
;
2.13. 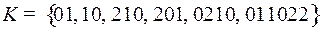 ;
;
2.14. 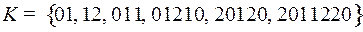 ;
;
2.15. 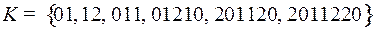 ;
;
2.16. 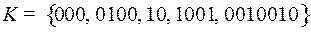 ;
;
2.17. 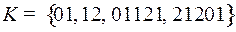 .
.
3. Выяснить, является ли слово 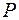 в алфавите
в алфавите 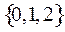 кодом сообщения в кодировании, задаваемом схемой:
кодом сообщения в кодировании, задаваемом схемой:
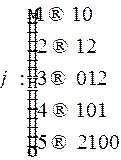
Если да, то выяснить, является ли слово 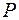 кодом ровно одного сообщения.
кодом ровно одного сообщения.
3.1. 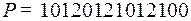 ;
;
3.2. 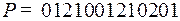 ;
;
3.3. 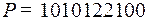 ;
;
3.4. 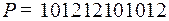 ;
;
3.5. 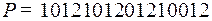 ;
;
3.6. 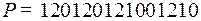 ;
;
3.7. 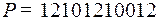 ;
;
3.8. 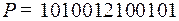 .
.
4. Выбрать максимальное по числу элементов подмножество 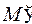 множества
множества 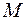 с условием, что двоичные разложения наименьшей длины чисел из
с условием, что двоичные разложения наименьшей длины чисел из 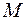 представляют собой префиксный код:
представляют собой префиксный код:
4.1. 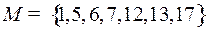 ;
;
4.2. 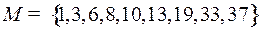 ;
;
4.3. 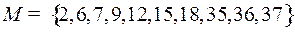 ;
;
4.4. 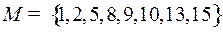 ;
;
4.5. 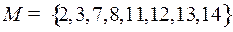 ;
;
4.6. 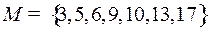 ;
;
4.7. 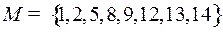 ;
;
4.8. 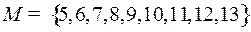 ;
;
4.9. 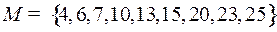 ;
;
4.10. 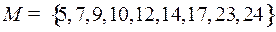 .
.
Приведем решение задачи 4.1.
Рассмотрим двоичные представления чисел из множества 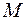 :
:
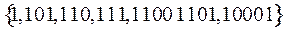 . Надо выбрать максимальное подмножество, чтобы эти двоичные представления образовали префиксный код. Если 1 войдет в
. Надо выбрать максимальное подмножество, чтобы эти двоичные представления образовали префиксный код. Если 1 войдет в 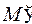 , то все остальные двоичные представления чисел не войдут. Если же 110 взять в качестве кодового слова, то
, то все остальные двоичные представления чисел не войдут. Если же 110 взять в качестве кодового слова, то 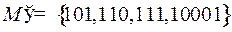 . Возьмем в качестве кодового слова 101, тогда
. Возьмем в качестве кодового слова 101, тогда 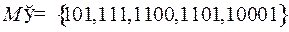 . Это подмножество
. Это подмножество 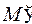 и будет максимальным.
и будет максимальным.
5. Для кода 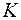 найти слово минимальной длины, декодируемое неоднозначно:
найти слово минимальной длины, декодируемое неоднозначно:
5.1. 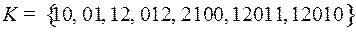 ;
;
5.2. 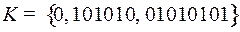 ;
;
5.3. 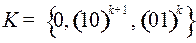
5.4. 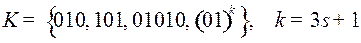 ;
;
5.5. 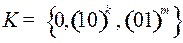 ;
;
5.6. 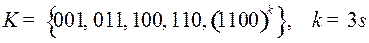 ;
;
5.7. 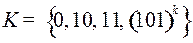 ;
;
5.8. 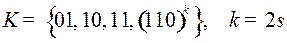 ;
;
5.9. 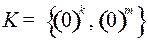 ;
;
5.10. 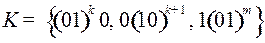 ;
;
5.11. 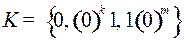 ;
;
5.12. 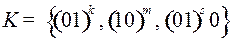 ;
;
5.13. 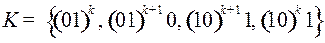 ;
;
5.14. 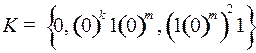 ;
;
5.15. 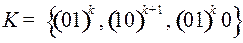 ;
;
5.16. 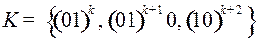 .
.
6. Построить двоичный префиксный код 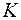 с заданной последовательностью
с заданной последовательностью 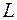 длин кодовых слов:
длин кодовых слов:
6.1. 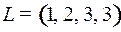 ;
;
6.2. 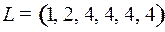 ;
;
6.3. 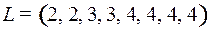 ;
;
6.4. 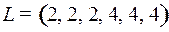 ;
;
6.5. 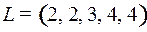 ;
;
6.6. 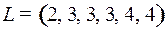 .
.
7. С помощью неравенства Макмиллана выяснить, может ли набор чисел 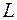 быть набором длин кодовых слов однозначно декодируемого кода в
быть набором длин кодовых слов однозначно декодируемого кода в 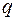 -значном алфавите:
-значном алфавите:
7.1. 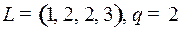 ;
;
7.2. 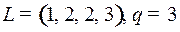 ;
;
7.3. 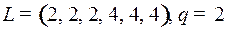 ;
;
7.4. 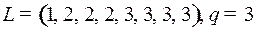 ;
;
7.5. 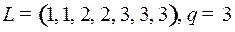 ;
;
7.6. 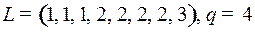 .
.
8. Для заданного набора длин кодовых слов указать набор вероятностей 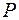 , при котором существует двоичный оптимальный код:
, при котором существует двоичный оптимальный код:
8.1. 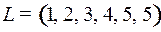 ;
;
8.2. 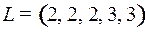 ;
;
8.3. 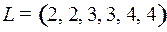 ;
;
8.4. 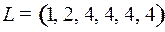 ;
;
8.5. 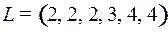 .
.
Рассмотрим решение задачи 8.5.
Построим кодовое дерево для кода 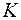 , на каждом шаге деля вероятности пополам (рис. 58).
, на каждом шаге деля вероятности пополам (рис. 58).
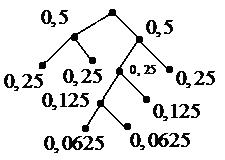
Рис. 58
Из рисунка ясно, что 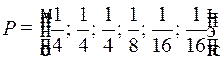 .
.
9. Выяснить, существует ли двоичный код с минимальной избыточностью, обладающий заданной последовательностью 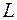 длин кодовых слов:
длин кодовых слов:
9.1. 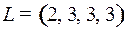 ;
;
9.2. 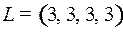 ;
;
9.3. 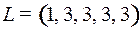 ;
;
9.4. 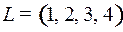 ;
;
9.5. 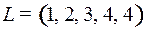 ;
;
9.6. 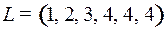 ;
;
9.7. 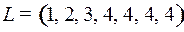 ;
;
9.8. 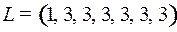 ;
;
9.9. 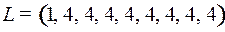 ;
;
9.10. 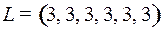 .
.
10. Построить по методу Хэмминга кодовое слово для сообщения 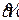 , состоящего только из информационных разрядов:
, состоящего только из информационных разрядов:
10.1. 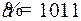 ;
;
10.2. 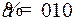 ;
;
10.3. 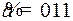 ;
;
10.4. 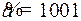 ;
;
10.5. 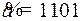 ;
;
10.6. 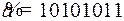 ;
;
10.7. 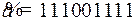 ;
;
10.8. 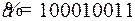 ;
;
10.9. 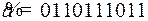 .
.
Разберем решение задачи 10.1.
Построим по методу Хэмминга кодовое слово для сообщения 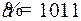 . Заполним информационные разряды, контрольные разряды, оказавшиеся между информационными, оставим свободными.
. Заполним информационные разряды, контрольные разряды, оказавшиеся между информационными, оставим свободными.
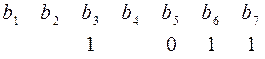
Между информационными разрядами разместилось 3 контрольных разряда, найдем их из уравнений 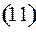 .
.
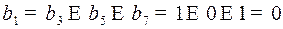
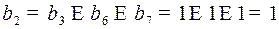
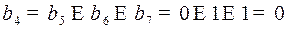
Заполнив контрольные разряды, получим кодовое слово в коде Хэмминга 0110011.
11. По каналу связи передавалось кодовое слово, построенное по методу Хэмминга для сообщения 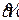 . После передачи по каналу связи, искажающему слово не более чем в одном разряде, было получено слово
. После передачи по каналу связи, искажающему слово не более чем в одном разряде, было получено слово 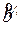 . Восстановить исходное сообщение:
. Восстановить исходное сообщение:
11.1. 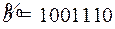 ;
;
11.2. 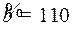 ;
;
11.3. 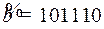 ;
;
11.4. 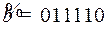 ;
;
11.5 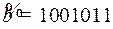 ;
;
11.6. 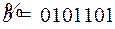 ;
;
11.7. 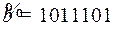 ;
;
11.8. 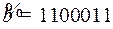 ;
;
11.9. 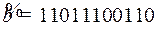 ;
;
11.10. 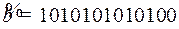 ;
;
11.11. 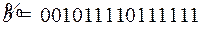 .
.
Рассмотрим решение задачи 11.1.
Декодируем вектор 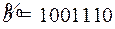 .
.
Длина слова 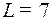 :
:
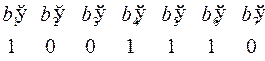
Числа от 1 до 7 кодируются трехзначными двоичными кодами и образуют три подмножества:
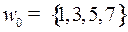 ,
, 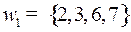 ,
, 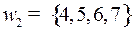
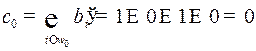
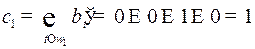
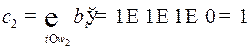
Номер разряда с ошибкой 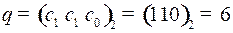 . Исправив шестой разряд, найдем посланное слово.
. Исправив шестой разряд, найдем посланное слово.
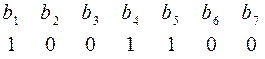 ,
,
удалим контрольные разряды 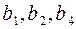 , получим
, получим 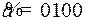 .
.
 2015-05-20
2015-05-20 6146
6146








