Пример

Имя	Вес (кг)	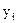Рост (см)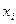
Вася
Коля
Петя

Оценим две модели:

М1: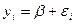

М2: 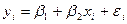Таким образом, необходимо найти 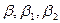для этих моделей.

Метод наименьших квадратов минимизирует величину RSS, т.е. величину .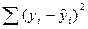

Рассмотрим модель М1: 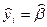, случайная компонента ε не прогнозируется.

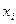
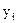
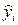
n				e
				= -
				= -
				= -

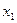
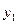
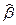
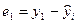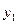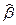
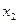
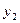
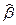
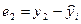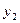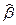
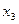
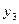
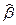
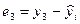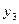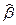
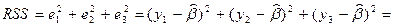
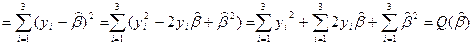
Рассмотрим слагаемые функции :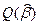

,

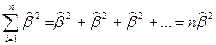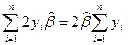, где .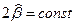

Следовательно функция 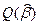имеет вид:

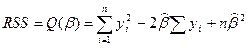для любого числа n в моделях без объясняющих переменных.

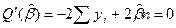
Разделим обе части равенства на -2n:

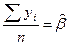
Соответственно .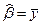

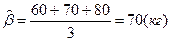
Теперь рассмотрим модель М2: 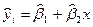, случайная компонента ε не прогнозируется.

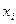
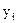
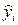
n				e
				= –
				= –
				= –

= =

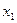
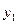
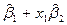
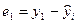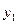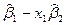
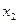
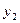
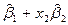
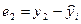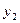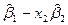
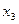
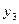
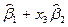
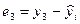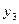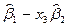
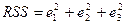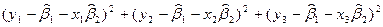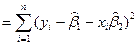
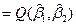
Как и в случае с М1, минимизируем функцию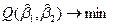

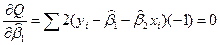
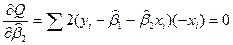
Разделим оба уравнения на -2.

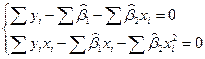
При этом, как и в модели 1, 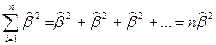, т.е.:

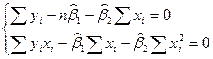
Разделим первое уравнение на n:

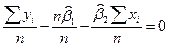
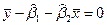
Выразим из последнего равенства :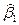

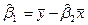
Подставим полученное значение во второе уравнение системы.

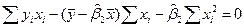
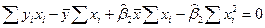
Сгруппируем слагаемые с 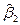в одной стороне и с 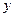в другой:

=

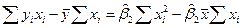
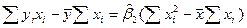
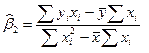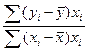
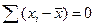
Следовательно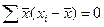

Прибавим к числителю и знаменателю на одно и то же число – ноль:

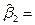
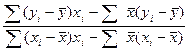
Внесем числитель под один знак суммы и то же проделаем со знаменателем:

Рассчитаем значение оценок параметров для примера:

n					(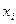
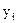
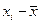
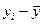
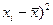
			-3,67	-10	13,4689
			-3,67		13,4689
			7,33		53,7289
S					80,6667
Среднее значение	173,67

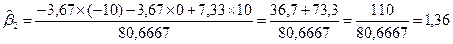
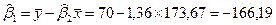
Таким образом, уравнение регрессии будет иметь вид: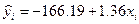

Из МНК

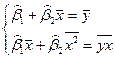
можно получить две другие формулы для нахождения параметра :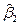

1.

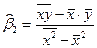
2.

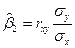
Оценка параметра 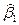а находится одинаковым способом во всех случаях:

.

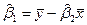Параметр 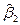называется коэффициентом регрессии и показывает, на сколько единиц в среднем изменится переменная 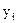при увеличении переменной 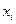на 1 единицу. Знак при коэффициенте регрессии показывает направление связи: при 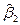< 0 – связь обратная, при 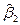> 0 – связь прямая.

Параметр 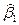формально представляет собой значение 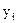при 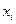= 0. Если 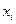не имеет или не может иметь нулевого значения, то 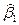не имеет смысла. Он может и не иметь экономического смысла. При 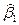<0 экономическая интерпретация может оказаться абсурдной.

Интерпретировать можно знак при параметре 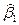. Если 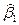>0, то относительное изменение результата происходит медленнее, чем изменение

Для случая модели множественной регрессии вида:

,

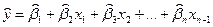где переменная 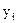оказывается зависимой от нескольких независимо влияющих не нее факторов, также применим МНК. При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии:

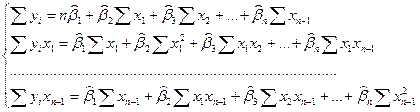
Решение этой системы может быть получено матричными способами. Интерпретация параметров – аналогично случаю парной регрессии с оговоркой «при фиксированном влиянии прочих факторов».