Дифференциальных уравнений

ЛЕКЦИЯ №4

Численное интегрирование дифференциальных уравнений

Задачи электротехники, приводящие к решению

дифференциальных уравнений

Обыкновенные дифференциальные уравнения(ОДУ)используются во всех областях электротехники чрезвычайно широко. Это объясняется тем, что большинство основных соотношений между электрическими и магнитными величинами устанавливают связь не между самими величинами, а скоростью их изменения во времени и пространстве. Как известно, физический смысл первой производной функции f(x) - 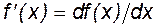- это скорость изменения функции в каждой ее точке. При написании уравнения математической модели электромагнита (глава 1, формула (1.3)) мы воспользовались соотношением 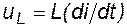. Это значит, что напряжение на катушке индуктивности зависит от скорости изменения тока, и чем она выше, тем напряжение больше. Здесь неизвестный ток входит в уравнение в виде своей производной. В электромеханике, кроме уравнений, связывающих только электрические величины, есть уравнения, связывающие электрические и механические величины, которые тоже являются дифференциальными, так как в основе их лежит второй закон Ньютона: 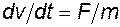, где 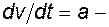ускорение, как производная от скорости по времени; F - механическая сила электрического происхождения, например, от взаимодействия двух токов.

Как составляется дифференциальное уравнение простой электрической цепи, описано в главе 1. Приведем пример составления системы дифференциальных уравнений более сложного устройства - трансформатора, имеющего две обмотки, намотанные на сердечник из электротехнической стали, по которому замыкается магнитный поток, пронизывающий обе обмотки. Этот магнитный поток называется потоком взаимоиндукции, а параметр трансформатора, связанный с ним - коэффициентом взаимоиндукции М (рис.4.1).

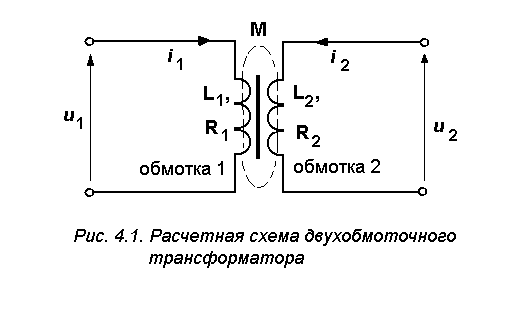По второму закону Кирхгофа для каждой из обмоток трансформатора можно записать уравнения равновесия напряжений:

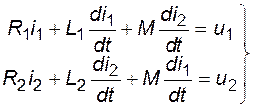, (4.1)

где R₁ и R₂ - активные сопротивления обмоток,

L₁ и L₂ - индуктивности обмоток,

М - коэффициент взаимоиндукции обмоток,

u₁ и u₂ – напряжения на обмотках.

Обозначив производные токов обмоток 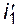и 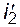, перенеся слагаемые без производных в правую часть, упорядочивая, получим:

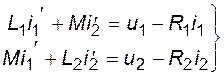(4.2)

или в матричной форме ,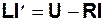

где ; ; ; ; .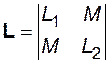

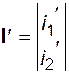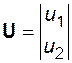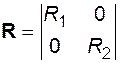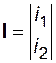Умножив обе части на обратную матрицу 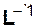(зная, что 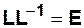- единичная матрица, имеющая тот же смысл в матричных операциях, что и единица), получим

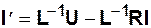. (4.3)

Мы получили в матричной форме систему дифференциальных уравнений трансформатора, записанную в форме Коши, то есть разрешенную относительно производных. Сравнив матричное уравнение (4.3) с уравнением (1.3), мы видим полное совпадение их структуры.

Интегрирование системы исходных дифференциальных уравнений электротехнического или электромеханического устройства, как правило, происходит с применением численных методов.