2015-05-20
833
8.2.1 Критерий Михайлова.
Критерий базируется на поведении кривой, которую описывает конец вектора (X(ω),Y(ω)) замкнутой системы при изменении частоты от 0 до +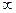 
.
Возьмём характеристический полином следующего вида:
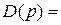
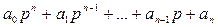(1)
Подставим в него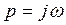 
и выделим вещественную и мнимую части.
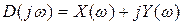
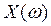- вещественная часть,
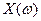
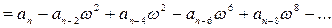
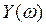- мнимая часть.
Изобразим годограф Михайлова выражения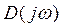 
на комплексной плоскости.
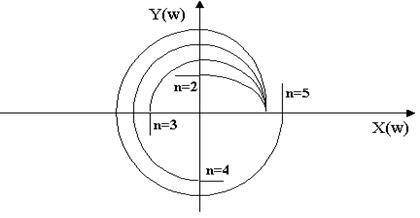
Рис. 10 Пример годографа Михайлова для устойчивых систем.
Берём значения 
и строим годограф. Для различных 
годограф имеет формы, представленные на рисунке. Эти годографы называются кривыми Михайлова. Кривая Михайлова строится по точкам, рассчитывается 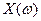и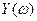 
для данной частоты, на кривой указываются значения частоты.
Формулировка критерия Михайлова
Чтобы САР была устойчивой, необходимо и достаточно, чтобы вектор D (jω) при изменении частоты от 0 до +∞ начал движение с точки, лежащей на положительной вещественной оси, и, вращаясь только против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов комплексной плоскости, повернувшись на угол n∙π/2, где n – степень характеристического уравнения D (jω)= 0
Другими словами, требуется, чтобы кривая Михайлова проходила последовательно 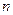квадрантов против часовой стрелки, всё время огибая начало координат и уходила в 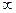в том квадранте, номер которого соответствует показателю степени полинома. Если это условие не выполняется, то система является неустойчивой.
 |
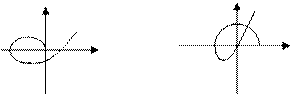Устойчивая Неустойчивая
Апериодическая Колебательная
граница устойчивости граница устойчивости
Рис. 11 Примеры годографа Михайлова для устойчивой и неустойчивой САУ, а так же системы, находящейся на границе устойчивости.
Другая формулировка критерия Михайлова (или следствие из критерия Михайлова):
Она состоит в использовании свойства перемежаемости корней многочленов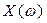 
и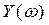 
.
Идя по кривой Михайлова от т.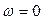 
в направлении возрастания частоты, мы выходим из оси 
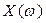, затем пересекаем ось 
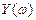, потом снова 
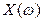и т. д.
Это значит, что корни уравнени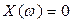й 
и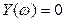 
должны следовать поочерёдно друг за другом.
Кривые 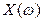и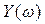 
имеют приблизительно такой вид:
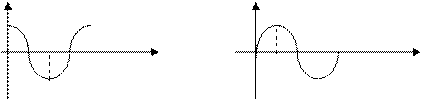
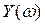
Перемежаться должны корни 
, 
, 
, 
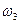,... Между ними должно быть следующее соотношение: > > >
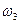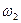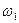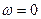
Условием устойчивости системы является перемежаемость корней полиномов вещественной и мнимой частей характеристического уравнения. Нарушение этого условия говорит о неустойчивости системы.
8.2.2 Критерий устойчивости Найквиста.
Данный критерий относится к частотным критериям. Как и критерий Михайлова, критерий Найквиста базируется на АФЧХ разомкнутой системы и даёт правила, согласно которым, по виду АФЧХ разомкнутой системы можно судить об устойчивости замкнутой системы. Соответственно существует две формулировки критерия Найквиста, в зависимости от поведения системы в разомкнутом состоянии.
а) система устойчива в разомкнутом состоянии
Если разомкнутая САУ устойчива, то для устойчивости замкнутой системы необходимо и достаточно. Чтобы АФЧХ разомкнутой системы не охватывала точку с координатами (-1; 0j).
Пусть передаточная функция разомкнутой системы такова:
, 
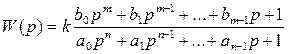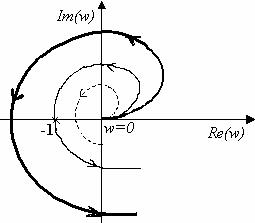
Рис. 12 Пример годографа Найквиста для устойчивых разомкнутых систем 
Система устойчива
Система на границе устойчивости
Система неустойчива
б) система с неустойчивой разомкнутой цепью
Пусть х.у. разомкнутой системы имеет l корней с положительной вещественной частью. Тогда для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы охватывала критическую точку с координатами (-1; 0j) против часовой стрелки на угол lπ.
Другими словами, АФЧХ разомкнутой системы может пересекать ось абсцисс левее точки -1 так, чтобы разность между числом положительных и отрицательных переходов была равна l /2. Или, при движении по направлению обхода кривой x.y. (при изменении ω от 0 до +∞), точка (-1, 0j) должна всегда находиться слева.
Положительный переход – сверху вних, отрицательный – снизу вверх.
