Геометрическими величинами называются величины, пропорциональные произведению нескольких (возможно, одной) длин. Геометрическая величина имеет вид
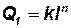 ,
,
где 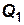 – рассматриваемая геометрическая величина;
– рассматриваемая геометрическая величина; 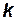 –коэффициент пропорциональности;
–коэффициент пропорциональности; 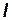 – длина;
– длина; 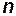 – целое число.
– целое число.
К геометрическим величинам относятся: длины 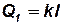 ; площади
; площади 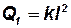 ; объёмы
; объёмы 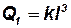 ; статические моменты длины
; статические моменты длины 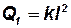 ; статические моменты площади
; статические моменты площади 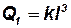 ; статические моменты объёма
; статические моменты объёма 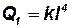 ; моменты инерции длины
; моменты инерции длины 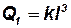 ; моменты инерции площади
; моменты инерции площади 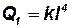 ; моменты инерции объёма
; моменты инерции объёма 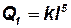 и т. п.
и т. п.
Обозначим систему тел и ограниченный этими телами поток жидкости в одном явлении через 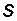 , а в другом – через
, а в другом – через 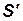 . Пусть в рассматриваемых явлениях жидкость движется относительно систем отсчета
. Пусть в рассматриваемых явлениях жидкость движется относительно систем отсчета 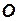 и
и 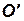 соответственно. Эти системы неподвижны относительно некоторой основной системы отсчета. Тела, ограничивающие потоки жидкости, в общем случае могут двигаться относительно тех же систем отсчета.
соответственно. Эти системы неподвижны относительно некоторой основной системы отсчета. Тела, ограничивающие потоки жидкости, в общем случае могут двигаться относительно тех же систем отсчета.
Обозначим через 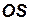 систему, состоящую из системы отсчета
систему, состоящую из системы отсчета 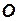 и системы
и системы 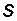 , а через
, а через 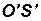 – систему, состоящую из системы отсчета
– систему, состоящую из системы отсчета 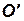 и системы
и системы 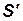 .
.
Две системы 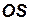 и
и 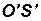 называются геометрически подобными, если между точками этих систем можно установить взаимно однозначное соответствие так, чтобы соответственные отрезки находились в постоянном отношении:
называются геометрически подобными, если между точками этих систем можно установить взаимно однозначное соответствие так, чтобы соответственные отрезки находились в постоянном отношении:
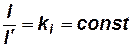 . . | (2.1) |
Если две системы (см. рис. 1) геометрически подобны, то
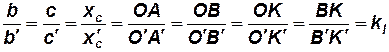 ,
,
откуда следует, что углы между соответственными отрезками равны и какая-либо фигура, составленная из точек первой системы, подобна геометрической фигуре, образованной точками второй системы.
Исходя из утверждения о том, что в геометрически подобных телах любая безразмерная комбинация, составленная из размерных величин, не изменяется, можно записать следующее равенство:
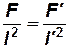 ,
,
где 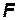 и
и 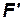 – соответственные площади подобных систем.
– соответственные площади подобных систем.
Из этого уравнения получим
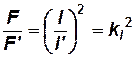 .
.
Таким образом, в геометрически подобных телах соответственные площади относятся как квадраты линейных размеров.
Аналогичным образом для отношений других геометрических величин в геометрически подобных телах находят следующие результаты:
отношение длин – 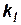 ;
;
отношение площадей – 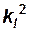 ;
;
отношение объёмов – 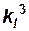 ;
;
отношение статических моментов длины – 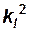 ;
;
отношение статических моментов площади – 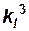 ;
;
отношение статических моментов объёма – 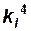 ;
;
отношение моментов инерции длины – 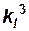 ;
;
отношение моментов инерции площади – 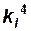 ;
;
отношение моментов инерции объёма – 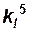 .
.
 2015-05-20
2015-05-20 1848
1848
