Динамическое подобие

Две кинематически подобные системы 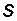и 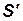называются динамически подобными, если отношение величин любых сил одной и той же природы (сил давления, трения и др.), действующих на соответственные элементы систем 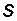и 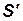в соответственные моменты времени, одинаково и равно отношению величин результирующих этих сил, т. е. соответственные многоугольники сил подобны и векторы сил одинаково ориентированы относительно своих систем отсчета. Если на выделенный элементарный объем жидкости действуют силы давления 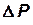, трения 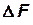и тяжести 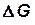(см. рис. 1), то при динамическом подобии для всех соответственных элементарных объемов

,

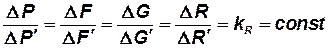(2.13)

где 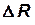и 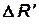– результирующие сил 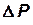, 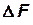и ,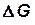

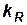– коэффициент подобия по силам динамически подобных систем.

Выразив величины результирующих сил по закону движения центра масс, получим

,

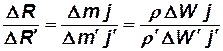где 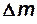и 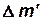– массы соответственных элементарных объемов жидкост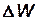и 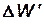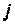и ,

и 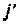– величины ускорений центров масс движущихся объемов жидкости.

Учитывая, что отношение геометрически подобных объемов равно отношению кубов соответственных линейных размеров, т. е.

,

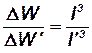и отношение соответственных ускорений согласно (2.12)

,

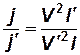находим

.

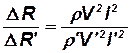Обозначим через 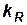масштаб сил динамически подобной системы

,

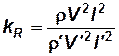(2.14)

где плотности и скорости можно взять в любых соот­ветственных точках.

Итак, в подобных гидромеханических явлениях соответственные длины, времена, величины скоростей и ускорений в сходственных точках и величины сил, действующих на соответственные элементы, в соответственные моменты времени находятся в постоянных отношениях, равных 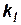, , 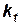, , 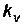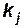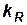. Кроме того, векторы скоростей, ускорений и сил в соответственных точках одинаково ориентированы относительно своих систем отсчета.