Арифметической прогрессией называется последовательность чисел 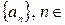 N, у которой каждый член, начиная со второго, равен предыдущему, сложенному с одним и тем же постоянным для данной последовательности числом
N, у которой каждый член, начиная со второго, равен предыдущему, сложенному с одним и тем же постоянным для данной последовательности числом 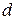 , т.е.
, т.е. 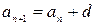
Формула 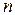 -ого члена арифметической прогрессии:
-ого члена арифметической прогрессии:
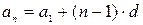 ,
,
где 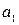 - первый член;
- первый член; 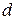 - разность прогрессии,
- разность прогрессии, 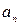 .- общий член.
.- общий член.
При любом 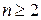 имеем:
имеем:
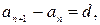
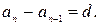
Таким образом (при 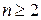 ),
),
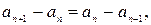 или
или 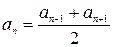 ,
,
т.е. каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.
Формула для общего члена арифметической прогрессии 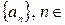 N связывает четыре величины:
N связывает четыре величины: 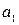 ,
, 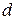 ,
, 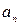 и
и 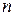 . Если три из них заданы, то из этой формулы можно найти четвертую величину. Приведем соответствующие формулы нахождения
. Если три из них заданы, то из этой формулы можно найти четвертую величину. Приведем соответствующие формулы нахождения 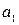 ,
, 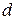 и
и 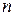 :
:
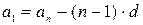 ;
; 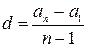 ;
; 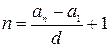 .
.
Сумма 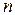 первых членов арифметической прогрессии:
первых членов арифметической прогрессии:
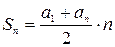 или
или  .
.
При 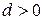 арифметическая прогрессия является монотонно возрастающей, а при
арифметическая прогрессия является монотонно возрастающей, а при 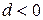 монотонно убывающей.
монотонно убывающей.
Геометрической прогрессией называется последовательность чисел 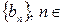 N, у которой каждый член, начиная со второго, получается из предыдущего умножением его на некоторое постоянное для этой последовательности число
N, у которой каждый член, начиная со второго, получается из предыдущего умножением его на некоторое постоянное для этой последовательности число 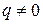 , т.е.
, т.е.
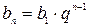 ,
, 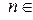 N.
N.
Число 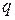 называется знаменателем геометрической прогресии,
называется знаменателем геометрической прогресии, 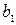 - первым членом;
- первым членом; 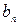 .- общим членом.
.- общим членом.
Любой член прогрессии можно выразить через соседние, как их среднее геометрическое: 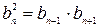 , где
, где 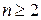 .
.
Сумма 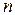 первых членов геометрической прогрессии:
первых членов геометрической прогрессии:
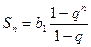 , если
, если 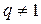 .
.
Для геометрической прогрессии 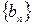 со знаменателем
со знаменателем 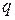 имеют место следующие свойства монотонности:
имеют место следующие свойства монотонности:
- прогрессия является возрастающей, если выполнено одно из следующих условий:
а) 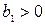 и и 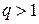 | б) 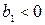 и и 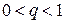 |
- прогрессия является убывающей, если выполнено одно из следующих условий:
а) 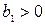 и и 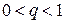 | б) 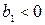 и и 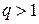 |
- если 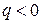 , то геометрическая прогрессия является знакопеременной: ее члены с нечетными номерами имеют тот же знак, что и ее первый член, а члены с четными номерами – противоположный ему знак. Знакопеременная геометрическая прогрессия не является монотонной.
, то геометрическая прогрессия является знакопеременной: ее члены с нечетными номерами имеют тот же знак, что и ее первый член, а члены с четными номерами – противоположный ему знак. Знакопеременная геометрическая прогрессия не является монотонной.
Сумма бесконечно убывающей геометрической прогрессии 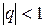 :
:
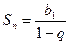 .
.
Процентом называется сотая часть числа.
В экономике есть понятие простых и сложных процентов.
Простые проценты начисляются по формуле:
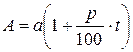 ,
,
а сложные - по формуле:
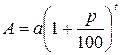 ,
,
где 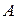 - нарощенный капитал;
- нарощенный капитал; 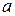 - основной капитал;
- основной капитал; 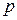 - процентная ставка;
- процентная ставка; 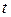 - время (число лет).
- время (число лет).
 2015-01-21
2015-01-21 2681
2681








