5.4. Доказать, что порядок элемента прямого произведения конечных групп равен наименьшему общему кратному порядков сомножителей.
5.5. Доказать, что если в абелевой группе подгруппы 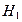 и
и 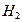 имеют взаимно простые порядки, то их сумма является прямой.
имеют взаимно простые порядки, то их сумма является прямой.
5.6. Пусть 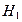 и
и 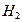 - такиеподгруппы группы, что
- такиеподгруппы группы, что 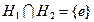 ,
, 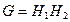 , и все элементы подгруппы
, и все элементы подгруппы 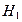 коммутируют с элементами подгруппы
коммутируют с элементами подгруппы 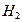 . Доказать, что
. Доказать, что 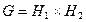 .
.
5.7. Пусть 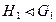 ,
, 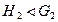 . Доказать, что
. Доказать, что 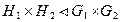 .
.
5.8. Пусть 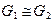 ,
, 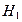 - нормальная подгруппа в
- нормальная подгруппа в 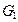 ,
, 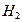 - нормальная подгруппа в
- нормальная подгруппа в 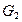 ,
, 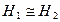 . Доказать, что
. Доказать, что 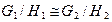 .
.
5.9. Пусть 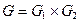 ,
, 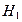 - нормальная подгруппа в
- нормальная подгруппа в 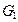 ,
, 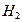 - нормальная подгруппа в
- нормальная подгруппа в 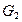 ,
, 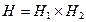 . Доказать, что
. Доказать, что 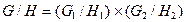 .
.
5.10. Доказать, что прямое произведение групп является абелевой группой тогда и только тогда, когда каждая из этих групп абелева.
5.11. Доказать, что центр прямого произведения равен прямому произведению центров сомножителей.
5.12. Найти классы сопряженности прямого произведения групп 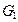 и
и 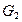 , если известны классы сопряженности групп
, если известны классы сопряженности групп 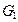 и
и 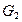 .
.
 2015-05-10
2015-05-10 415
415







