Теория метода. Проверка зависимости углового ускорения от момента действующих сил

Проверка зависимости углового ускорения от момента действующих сил. На маятник действуют сила натяжения нити 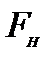и сила сопротивления 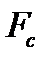, обусловленная трением в подшипниках и сопротивлением воздуха. (Сила тяжести маятника уравновешена силой реакции стойки 13, на которую укреплен маятник).

Моменты сил 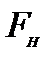и 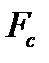обозначим через 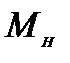и .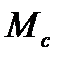

С учетом знаков моментов сил 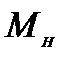и 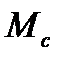согласно основному закону динамики вращательного движения тел (2.1)

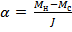(2.4)

Момент инерции 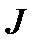маятника при неизменном расположении цилиндрических грузов 5 на стержнях и момент сил сопротивления 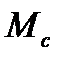, если пренебречь зависимостью силы сопротивления от скорости, постоянны. Поэтому проверка зависимости (2.2) сводится к проверке линейной зависимости углового ускорения 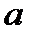от момента силы натяжения нити 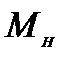(2.4).

Момент силы натяжения 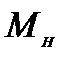можно изменять, подвешивая к свободному концу нити грузы 8 с разной массой 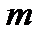и наматывая нить на разные шкивы.

Экспериментально определенные значения высоты падения груза 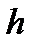, времени падения 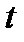и заданные значения масс грузов 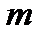и диаметров шкивов 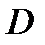позволяют определить угловое ускорение маятника 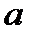(см. п.п. 1.3,г в «Заданиях …») и момент силы натяжения 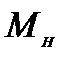(см. п.п. 1.6 в «Заданиях …») при различных 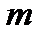и 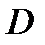, и, построив график зависимости 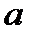от 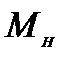, убедиться в справедливости зависимости (2.4).

Определение момента инерции маятника J и момента сил сопротивления 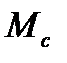. График зависимости углового ускорения от момента силы натяжения 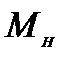позволяет определить момент инерции маятника J и момент сил сопротивления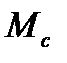

Сопоставив уравнение (2.4) с уравнением прямой в виде

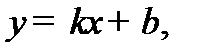
заключаем, что угловой коэффициент 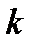, равный тангенсу угла наклона прямой α(M), в нашем случае равен:

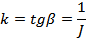
Отсюда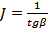

Используя определение тангенса угла, получим:

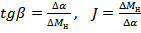(2.5)

где Δ 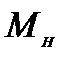– выбранный интервал момента силы натяжения, 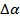- соответствующий Δ 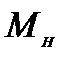интервал углового ускорения, определенный по графику зависимости 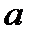от .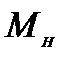

Отрезок 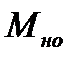, отсекаемый прямой на оси 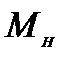, является моментом силы натяжения, при котором α = 0, т.е. моментом силы натяжения, при котором маятник начинает вращаться. Поэтому согласно уравнению (2.4)

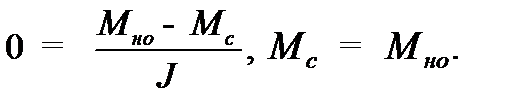(2.6)

(Из (2.4) следует, что при 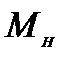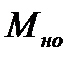маятник должен вращаться с угловым

ускорением 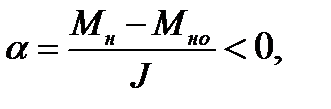т.е. в обратную сторону, но этого не будет, т.к.

сила сопротивления 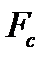и 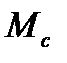возникают только при действии 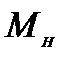, причем при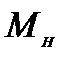 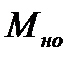момент сил сопротивления = ).

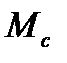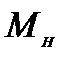Таким образом, график зависимости α от 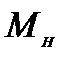позволяет определить момент инерции маятника J при выбранном расстоянии грузов 5 до оси вращения (2.5) и момент сил сопротивления 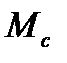(2.6).