СИММЕТРИЧНЫЙ РЕЖИМ РАБОТЫ ТРЕХФАЗНОЙ ЦЕПИ
Соберите схему с симметричной резистивной нагрузкой, включив в каждую фазу треугольника резистор с номинальным сопротивлением 1 кОм (рис. 5.2).
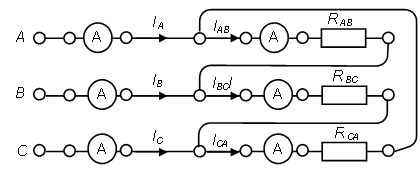 Рис. 5.2.
Рис. 5.2.
|
В качестве приемников используются три резистора: 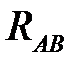 ,
, 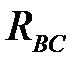 ,
, 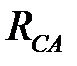 с номинальным сопротивлением каждого 1 кОм. Для измерения фазных токов нагрузки предусмотрите включение амперметров последовательно с резисторами в фазах нагрузки. Для измерения линейных токов включите три амперметра в линейные провода. Измерение напряжений на элементах схемы производите поочередным подключением вольтметра к различным участкам цепи.
с номинальным сопротивлением каждого 1 кОм. Для измерения фазных токов нагрузки предусмотрите включение амперметров последовательно с резисторами в фазах нагрузки. Для измерения линейных токов включите три амперметра в линейные провода. Измерение напряжений на элементах схемы производите поочередным подключением вольтметра к различным участкам цепи.
Измерьте напряжения и токи, указанные в табл. 5.2. Подключая токовую цепь ваттметра сначала в фазу А, а цепь напряжения – на напряжение UAB, затем токовую цепь в фазу C, а цепь напряжения – на напряжение UCB, измерьте две активные мощности и вычислите суммарную активную мощность. (Для переключения ваттметра из одной цеп в другую, также как и амперметра, используйте специальный коммутационный мини блок «амперметр» и пару проводников с коаксиальным разъёмом!). Результаты измерений занесите в табл. 5.2.
По данным опыта проверьте соотношение между линейными и фазными токами. Постройте топографическую диаграмму напряжений и векторную диаграмму токов.
Считая известными линейные напряжения источника и параметры (сопротивления) фаз приемника, рассчитайте фазные и линейные токи и активные мощности приемника. Результаты расчетов занесите в табл. 5.2. Проверьте баланс активных мощностей.
При соединении фаз приемника по схеме «треугольник» сопротивления каждой фазы 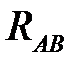 ,
, 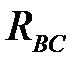 и
и 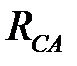 подключаются к линейному напряжению источника, которой равно фазному напряжению приемника
подключаются к линейному напряжению источника, которой равно фазному напряжению приемника 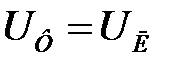 .
.
Фазные токи определяются по закону Ома:
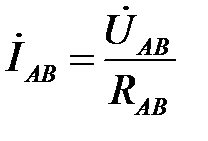 ;
; 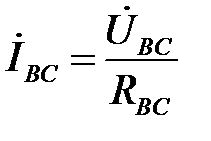 ;
; 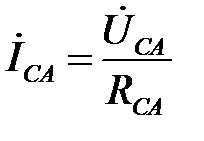 .
.
Линейные токи определяются по первому закону Кирхгофа как разность фазных токов:
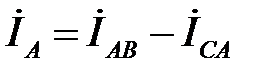 ;
; 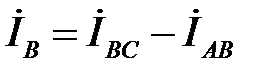 ;
; 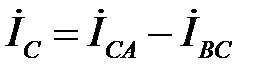 .
.
При симметричных напряжениях 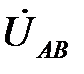 ,
, 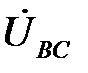 ,
, 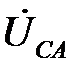 и симметричной резистивной нагрузке
и симметричной резистивной нагрузке 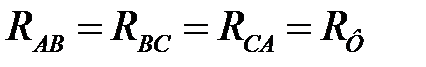 фазные и линейные токи будут также симметричны и их действующие значения могут быть определены по формулам:
фазные и линейные токи будут также симметричны и их действующие значения могут быть определены по формулам:
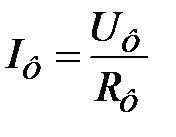 ;
; 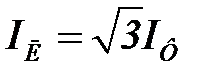 .
.
Построение топографической диаграммы напряжений делается в следующей последовательности. Вектор одного из фазных напряжений приемника 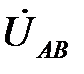 ,
, 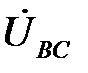 или
или 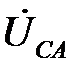 строится в масштабе напряжений в произвольном направлении. Так на рис. 5.3 вектор
строится в масштабе напряжений в произвольном направлении. Так на рис. 5.3 вектор 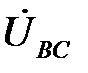 отложен горизонтально. Из конца вектора
отложен горизонтально. Из конца вектора 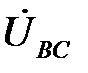 проводим дугу окружности радиусом
проводим дугу окружности радиусом 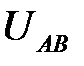 , а из начала – радиусом
, а из начала – радиусом 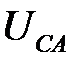 . Точка пересечения дуг определяет положение потенциала точки А.
. Точка пересечения дуг определяет положение потенциала точки А.
Векторная диаграмма токов строится в масштабе токов вместе с топографической диаграммой напряжений. При резистивной нагрузке фазные токи
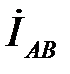 ,
, 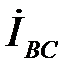 и
и 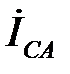 совпадают по фазе соответственно с фазными напряжениями
совпадают по фазе соответственно с фазными напряжениями 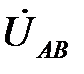 ,
, 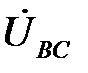 и
и 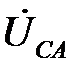 (рис. 5.3). Линейные токи
(рис. 5.3). Линейные токи 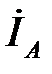 ,
, 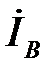 и
и 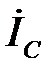 находятся как геометрическая разность векторов фазных токов.
находятся как геометрическая разность векторов фазных токов.
В случае резистивного приемника реактивная мощность равна нулю, а активная мощность равна полной мощности. В симметричной трехфазной цепи мощности всех фаз равны между собой. При соединении фаз приемника по схеме «треугольник» активная мощность может быть рассчитана по формулам:
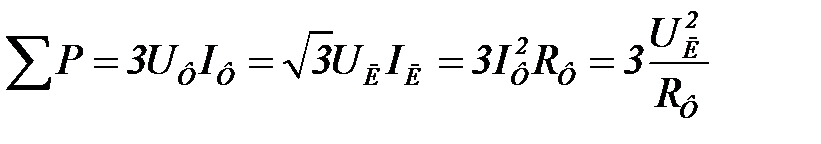 .
.
При смешанной (активно-индуктивной или активно-емкостной) нагрузке в симметричной трехфазной цепи:
Активная мощность
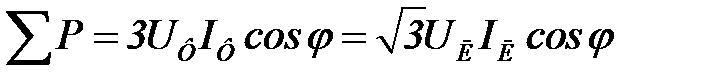 ,
,
где φ – сдвиг по фазе между фазными токами и напряжениями приемника.
Реактивная мощность
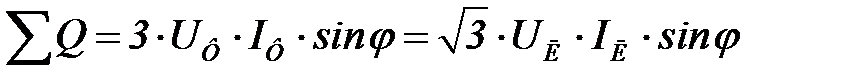 .
.
Полная мощность
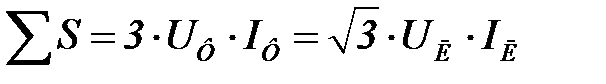 .
.
 2015-05-10
2015-05-10 241
241








