Лабораторная работа 1-5
ИЗУЧЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ
ПРАВИЛЬНОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
Цель работы: рассматриваются понятия тензора инерции, эллипсоида инерции при вращении твердого тела.
· Задача работы: оценка моментов инерции твердых тел правильной геометрической формы методом крутильных колебаний.
· Приборы и принадлежности: унифилярный подвес, набор образцов (тел правильной геометрической формы), штангенциркуль.
I. Проводим опыт и вычисляем период колебаний крутильного маятника формы куба (размерами a=0,048м, b=0,048м, c=0,048м) по формуле 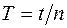 , где
, где 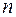 – число колебаний,
– число колебаний, 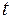 - их время. Результаты заносим в таблицу 1:
- их время. Результаты заносим в таблицу 1:
Таблицу 1: Сводная таблица результатов измерений периода колебаний крутильного маятника 1 и вычисления некоторых параметров, необходимых для обработки результатов измерения.
| Образец № 1 (Куб) | |||||||||||||||
| a, m | 0,048 | b, m | 0,048 | c, m | 0,048 | ||||||||||
| a2, m2 | 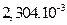
| b2, m2 | 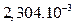
| c2, m2 | 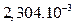
| r2, m2 | 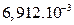
| ||||||||
| a4, m4 | 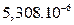
| b4, m4 | 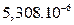
| c4, m4 | 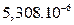
| ||||||||||
| № | Tx, с | T2x | T2x - <T2x> | (T2x - <T2x>)2 | Ty с | T2y | T2y - <T2y> | (T2y - <T2y>)2 | Tz, с | T2z | T2z - <T2z> | (T2z - <T2z>)2 | Tэксп, с | ||
| 0,8238 | 0,6786 | 0,0624 | 3,894. 
| 0,8246 | 0,68 | 2,5. 
| 6,25. 
| 0,8275 | 0,6848 | 0,0344 | 1,183. 
| 0,775 | |||
| 0,7745 | 0,5999 | 0,0515 | 2,657. 
| 0,7725 | 0,5968 | 1,102. 
| 1,214. 
| 0,7727 | 0,5971 | -0,0533 | 2,841. 
| 0,775 | |||
| 0,7745 | 0,5999 | 0,0515 | 2,657. 
| 0,8238 | 0,6786 | 2,362. 
| 5,579. 
| 0,8283 | 0,6861 | 0,0357 | 1,274. 
| 0,774 | |||
| 0,7754 | 0,6012 | 0,015 | 2,25. 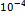
| 0,7733 | 0,598 | 1,024. 
| 1,049. 
| 0,8283 | 0,6861 | 0,0357 | 1,274. 
| 0,774 | |||
| 0,7754 | 0,6012 | 0,015 | 2,25. 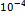
| 0,7725 | 0,5968 | 1,102. 
| 1,214. 
| 0,7733 | 0,598 | -0,0524 | 2,745. 
| 0,825 | |||
| <T2x> | 0,6162 | 
| 5,658. 
| <T2y> | 0,63 | 
| 15,306. 
| <T2z> | 0,6504 | 
| 9,317. 
| ||||
| Образец № 3 | |||||||||||||||
| a, m | 0,04 | b, m | 0,04 | c, m | 0,07 | ||||||||||
| a2, m2 | 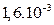
| b2, m2 | 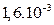
| c2, m2 | 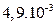
| r2, m2 | 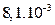
| ||||||||
| a4, m4 | 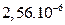
| b4, m4 | 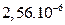
| c4, m4 | 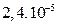
| ||||||||||
| № | Tx, с | T2x | T2x - <T2x> | (T2x - <T2x>)2 | Ty с | T2y | T2y - <T2y> | (T2y - <T2y>)2 | Tz, с | T2z | T2z - <T2z> | (T2z - <T2z>)2 | Tэксп, с | ||
| 0,8292 | 0,6876 | -0,0369 | 1,362. 
| 0,8318 | 0,6919 | 1,2. 
| 1,44. 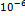
| 0,7783 | 0,6058 | 0,0361 | 1,303. 
| 0,82 | |||
| 0,8292 | 0,6876 | -0,0369 | 1,362. 
| 0,83 | 0,6889 | -1,8. 
| 3,24. 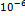
| 0,7282 | 0,5303 | -0,0439 | 1,927. 
| 0,7709 | |||
| 0,8831 | 0,7799 | 0,0554 | 3,069. 
| 0,8327 | 0,6934 | 2,7. 
| 7,29. 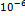
| 0,7783 | 0,6058 | 0,0361 | 1,303. 
| 0,7709 | |||
| 0,8831 | 0,7799 | 0,0554 | 3,069. 
| 0,8309 | 0,6904 | -3. 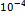
| 9. 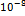
| 0,7273 | 0,529 | -0,0452 | 2,043. 
| 0,7692 | |||
| 0,8292 | 0,6876 | -0,0369 | 1,362. 
| 0,83 | 0,6889 | -1,8. 
| 3,24. 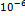
| 0,7746 | 0,6 | 0,0258 | 6,656. 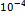
| 0,7718 | |||
| <T2x> | 0,7245 | 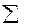
| 1,022. 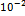
| <T2y> | 0,6907 | 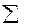
| 1,53. 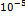
| <T2z> | 0,5742 | 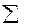
| 7,242. 
| ||||
II. Проводим опыт и вычисляем период колебаний крутильного маятника формы параллелепипеда (размерами a=0,05м, b=0,03м, c=0,07м) по формуле 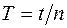 , где
, где 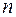 – число колебаний,
– число колебаний, 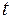 - их время. Результаты заносим в таблицу 2:
- их время. Результаты заносим в таблицу 2:
Таблицу 1: Сводная таблица результатов измерений периода колебаний крутильного маятника 2 и вычисления некоторых параметров, необходимых для обработки результатов измерения.
| Образец № 2 | |||||||||||||||
| a, m | 0,05 | b, m | 0,03 | c, m | 0,07 | ||||||||||
| a2, m2 | 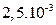
| b2, m2 | 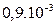
| c2, m2 | 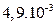
| r2, m2 | |||||||||
| a4, m4 | 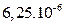
| b4, m4 | 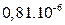
| c4, m4 | 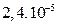
| ||||||||||
| № | Tx, с | T2x | T2x - <T2x> | (T2x - <T2x>)2 | Ty с | T2y | T2y - <T2y> | (T2y - <T2y>)2 | Tz, с | T2z | T2z - <T2z> | (T2z - <T2z>)2 | Tэксп, с | ||
| 0,7982 | 0,6371 | -0,0326 | 1,063. 
| 0,8427 | 0,7101 | -0,036 | 1,296. 
| 0,7809 | 0,6098 | 0,0367 | 1,347. 
| 0,8123 | |||
| 0,7967 | 0,6347 | -0,035 | 1,125. 
| 0,8427 | 0,7101 | -0,036 | 1,296. 
| 0,7783 | 0,6058 | 0,0327 | 1,069. 
| 0,7625 | |||
| 0,7967 | 0,6347 | -0,035 | 1,125. 
| 0,8408 | 0,7069 | -0,0392 | 1,537. 
| 0,725 | 0,5256 | -0,0475 | 2,256. 
| 0,7625 | |||
| 0,8492 | 0,7211 | 0,0514 | 2,642. 
| 0,8954 | 0,8017 | 0,0556 | 3,091. 
| 0,725 | 0,5256 | -0,0475 | 2,256. 
| 0,7636 | |||
| 0,8492 | 0,7211 | 0,0514 | 2,642. 
| 0,8954 | 0,8017 | 0,0556 | 3,091. 
| 0,7738 | 0,5988 | 0,0257 | 6,6. 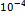
| 0,7617 | |||
| <T2x> | 0,6697 | 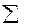
| 8,597. 
| <T2y> | 0,7461 | 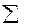
| 1,031. 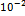
| <T2z> | 0,5731 | 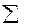
| 7,588. 
| ||||
· Находим среднее значение квадрата периода 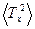 :
:
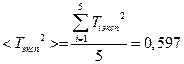
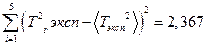
· Вычисляем среднее квадратичное 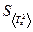 по формуле:
по формуле:
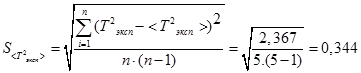
· Значение параметра Стьюдента: k = n -1 = 4; p = 0,95 à 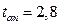
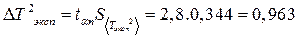
· Записываем ответ экспериментального периода в виде: 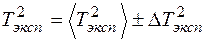 = 0,616
= 0,616 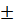 0,963.
0,963.
· Вычисляем среднее квадратичное 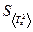 ,
, 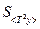 ,
, 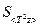 по формуле:
по формуле:
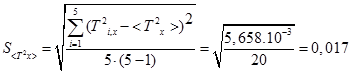
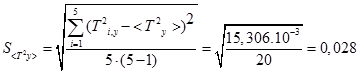
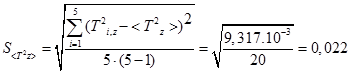
· 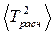 определяется по формуле:
определяется по формуле:
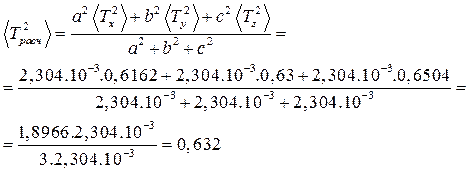
· Для расчета доверительного интервала находят среднее квадратичное величины 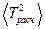 :
:
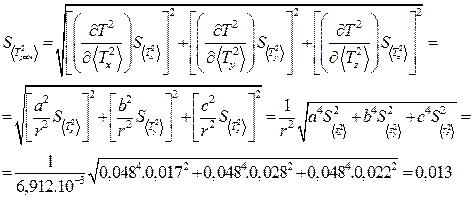
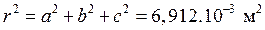
à 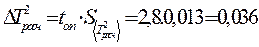
· Записываем результат в виде: 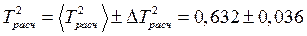
· Сравниваем:
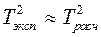
III. Проводим опыт и вычисляем период колебаний крутильного маятника формы параллелепипеда (размерами a=0,04м, b=0,04м, c=0,07м) по формуле 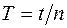 , где
, где 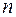 – число колебаний,
– число колебаний, 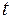 - их время. Результаты заносим в таблицу 1:
- их время. Результаты заносим в таблицу 1:
Таблицу 3: Сводная таблица результатов измерений периода колебаний крутильного маятника 3 и вычисления некоторых параметров, необходимых для обработки результатов измерений:
| Образец № 3 | |||||||||||||||
| a, m | 0,04 | b, m | 0,04 | c, m | 0,07 | ||||||||||
| a2, m2 | 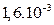
| b2, m2 | 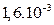
| c2, m2 | 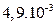
| r2, m2 | 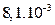
| ||||||||
| a4, m4 | 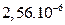
| b4, m4 | 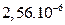
| c4, m4 | 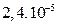
| ||||||||||
| № | Tx, с | T2x | T2x - <T2x> | (T2x - <T2x>)2 | Ty с | T2y | T2y - <T2y> | (T2y - <T2y>)2 | Tz, с | T2z | T2z - <T2z> | (T2z - <T2z>)2 | Tэксп, с | ||
| 0,8292 | 0,6876 | -0,0369 | 1,362. 
| 0,8318 | 0,6919 | 1,2. 
| 1,44. 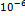
| 0,7783 | 0,6058 | 0,0361 | 1,303. 
| 0,82 | |||
| 0,8292 | 0,6876 | -0,0369 | 1,362. 
| 0,83 | 0,6889 | -1,8. 
| 3,24. 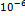
| 0,7282 | 0,5303 | -0,0439 | 1,927. 
| 0,7709 | |||
| 0,8831 | 0,7799 | 0,0554 | 3,069. 
| 0,8327 | 0,6934 | 2,7. 
| 7,29. 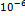
| 0,7783 | 0,6058 | 0,0361 | 1,303. 
| 0,7709 | |||
| 0,8831 | 0,7799 | 0,0554 | 3,069. 
| 0,8309 | 0,6904 | -3. 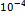
| 9. 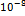
| 0,7273 | 0,529 | -0,0452 | 2,043. 
| 0,7692 | |||
| 0,8292 | 0,6876 | -0,0369 | 1,362. 
| 0,83 | 0,6889 | -1,8. 
| 3,24. 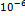
| 0,7746 | 0,6 | 0,0258 | 6,656. 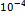
| 0,7718 | |||
| <T2x> | 0,7245 | 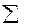
| 1,022. 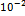
| <T2y> | 0,6907 | 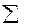
| 1,53. 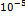
| <T2z> | 0,5742 | 
| 7,242. 
| ||||
 2015-05-10
2015-05-10 633
633






