Задание 4. 1. Найти общее и одно частное решение системы

1. Найти общее и одно частное решение системы: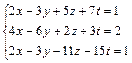

> eq:={2*x-3*y+5*z+7*t=1, 4*x-6*y+2*z+3*t=2,

2*x-3*y-11*z-15*t=1}:

> s:=solve(eq,{x,y,z});

s:={ 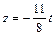, y = y, }

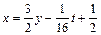Для нахождения частного решения следует выполнить подстановку конкретного значения одной из переменных при помощи команды subs:

> subs({y=1,t=1},s);

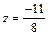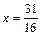{ , , 1=1}

2. Решить матричное уравнение: АX = В; где ,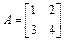

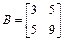
> A:=matrix([[1,2],[3,4]]):

> B:=matrix([[3,5],[5,9]]):

> X:=linsolve(A,B);

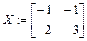
3. Дана матрица 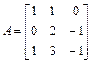. Найти ее ранг, дефект: d (A)= n – r (A), где n – размерность квадратной матрицы, r – ее ранг. Найти ядро А. Наберите:

> A:=matrix([[1,1,0],[0,2,-1],[1,3,-1]]):

> r(A):=rank(A);

r(A):=2

> d(A):=rowdim(A)-r(A);

d(A):=1

> k(A):=kernel(A);

k(A):={[-1,1,2]}