Краткие сведения из теории

Лабораторная работа №6 Минимизация логических функций

Цель работы: приобретение студентами практических навыков в проектировании логических функций, их минимизация и составление логических схем устройств.

Краткие сведения из теории

Логическая функция – это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.

Каждая логическая функция может быть задана большим количеством различных по виду функций. Но даже любую достаточно сложную логическую функцию можно реализовать, имея относительно простой набор базовых логических операций. Наиболее известный базис – это набор функций «и», «или», «не».

Для операций конъюнкции, дизъюнкции и инверсии определены законы, позволяющие производить тождественные (равносильные) преобразования логических выражений:

1. закон двойного отрицания: ;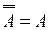

2. коммутативность конъюнкции: ;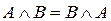

3. коммутативность дизъюнкции: ;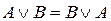

4. ассоциативность конъюнкции: ;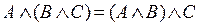

5. ассоциативность дизъюнкции: ;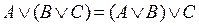

6. дистрибутивность конъюнкции относительно дизъюнкции :
;

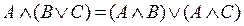7. дистрибутивность дизъюнкции относительно конъюнкции:
;

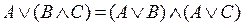8. законы идемпотентности: ,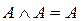
;

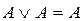9. закон исключенного третьего: ;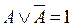

10. закон непротиворечия: ;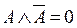

11. законы поглощения 1: ,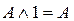
,
,
;

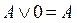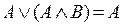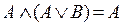12. законы де Моргана: ,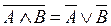
;

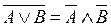13. законы склеивания: ,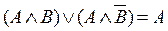
;

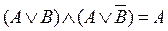14. замена импликации: ;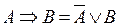

15. правила Порецкого: ,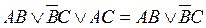

;

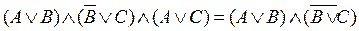16. правила свертки: ,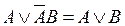

.

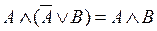Основываясь на законах, можно выполнять упрощение сложных логических выражений.

Исходными, из соображений удобства последующих преобразований, приняты следующие две канонические формы представления функций: совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).

Прежде чем перейти к СДНФ и СКНФ введем некоторые понятия.

Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые.

Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые.

Всякую дизъюнкцию элементарных конъюнкций называют дизъюнктивной нормальной формой, то есть ДНФ.

Например, выражение 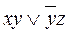является ДНФ.

Всякую конъюнкцию элементарных дизъюнкций называют конъюнктивной нормальной формой, то есть КНФ [15].

Например, выражение 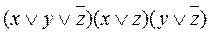является КНФ.

Совершенной ДНФ (СДНФ) называется ДНФ, в которой нет равных элементарных конъюнкций, и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с отрицанием).

Например, выражение 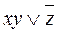является ДНФ, но не является СДНФ; выражение 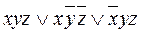является СДНФ.

Совершенной КНФ (СКНФ) называется КНФ, в которой нет равных элементарных дизъюнкций, и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с отрицанием).

Например, выражение .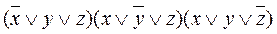

Приведу алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:

а). переход от произвольного задания функции к ДНФ

Этот переход сводится к опусканию общих для нескольких переменных инверсий, раскрытию скобок и объединению, если они возникают, одинаковых членов с использованием законов:

1. законы идемпотентности: ,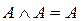
;

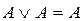2. закон исключенного третьего: ;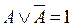

3. закон непротиворечия: ;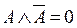

Например:

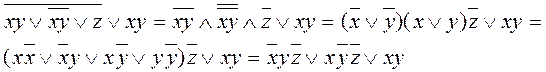
б). переход от ДНФ к КНФ

Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения. Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:

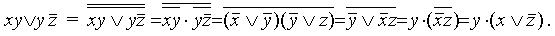
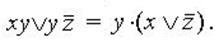Второй способ перехода от ДНФ к КНФ – использование дистрибутивного закона:

в). переход от КНФ к ДНФ

Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения):

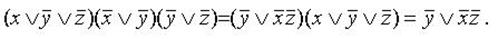
г). переход от КНФ к СКНФ

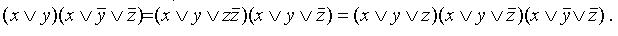Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной, например, z, то добавляем в нее выражение 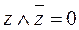(это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона:

д). переход от ДНФ к СДНФ

Если в какой-то простой конъюнкции недостает переменной, например, z, то умножаем неполную конъюнкцию на выражение вида 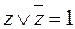, после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:

е). 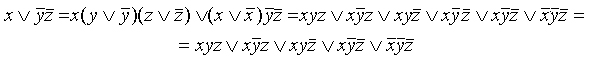переход к СДНФ и СКНФ с помощью таблиц истинности

Для получения СДНФ и СКНФ из таблиц истинности необходимо выполнить следующие 4 пункта алгоритма:

СДНФ

СКНФ

1. Конструирование СДНФ и СКНФ начинается с таблицы истинности.

2. Отметим те строки таблицы, выходы которых равны

3. Выписываем для каждой отмеченной строки комбинацию переменных через знак

конъюнкция (&)

дизъюнкция (V)

Знаки операции отрицания расставляем следующим образом:

если переменная равна 1, то запишем саму эту переменную, если же она равна 0, то запишем ее отрицание.

если переменная равна 0, то запишем саму эту переменную, если же она равна 1, то запишем ее отрицание.

4. Все полученные выражения связываем операцией

дизъюнкции

конъюнкции

Получив СДНФ или СКНФ, можно составить электронную схему, реализующую данную логическую функцию. Для ее постороения требуется 3 логических элемента:

инвертор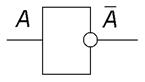
конъюнктор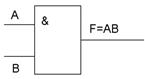
дизъюнктор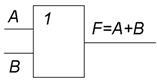

Но чаще всего СДНФ содержит много слагаемых и задача заключается в том, чтобы уменьшить их число и упростить логическое выражение. Для упрощения логических функций можно использовать законы логики, приведенные выше. С этой же целью были разработаны и специальные методы, речь о которых пойдет далее.